Enunciado
Ciência dos Materiais - Callister - Ciência e Engenharia de Materiais. Uma Introdução- Ed: 8º - Capítulo 18.Perguntas e Problemas - Ex. 47
Observamos na Seção 12.5 (Figura12.22) que no FeO (wusita) os íons de ferro podem existir tanto no estado quanto no . A quantidade de cada um desses tipos de íons depende da temperatura e da pressão ambiente do oxigênio. Além disso, também foi observado que para manter a eletroneutralidade, uma lacuna de será criada para cada dois íons de formados; consequentemente, para refletir a existência dessas lacunas, a fórmula da wusita é representada com frequência como , em que x é alguma pequena fração, menor que a unidade.
Nesse material não estequiométrico, a condução é eletrônica e, de fato, ele se comporta como um semicondutor do tipo p. Ou seja, os íons atuam como receptores eletrônicos sendo relativamente fácil excitar um elétron da banda de valência para um estado receptor , com a consequente formação de um buraco. Determine a condutividade elétrica de wusita que tem mobilidade dos buracos de e para qual o valor de x é de 0,060. Considere que os estados receptores estejam saturados (i.e. existe um buraco para cada íon ). A wusita apresenta estrutura cristalina do cloreto de sódio com comprimento da aresta da célula unitária de 0,437 nm.
Passo 1
Pra resolver essa questão vamos usar a fórmula da condutividade para um material semicondutor do tipo p:
Nós sabemos a carga do elétron e sabemos a mobilidade dos buracos.
O que a gente precisa então calcular primeiro é a concentração de portadores , que nada mais é do que o número de buracos. Essa concentração é dada por m³, então vamos precisar olhar pra estrutura atômica do cloreto de sódio para chegar em um valor!
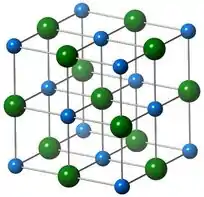
Onde os íons de carga positiva são os azuis. Olhando pra figura a gente pode contar átomos de !
Como ele não é estequiométrico:
Passo 2
Vamos calcular então o volume da célula unitária:
Agora vamos ver quantas células unitárias existem em 1 m³:
Multiplicando pelo número de íons (que é igual ao número de buracos):
Passo 3
Agora que temos o número de buracos podemos calcular a condutividade do material!