Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Ciência dos Materiais - Callister - Ciência e Engenharia de Materiais. Uma Introdução- Ed: 8º - Capítulo 3.Perguntas e Problemas - Ex. 14

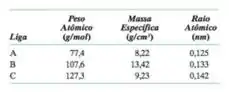
O peso atômico, a massa específica e o raio atômico para três liga hipotética estão listados na tabela a seguir. Para cada uma delas, determine se a estrutura cristalina é CFC, CCC ou cúbica simples e, então, justifique sua determinação.

Passo 1

Pra resolver essa questão, precisamos calcular o volume da célula unitária de cada liga à partir da massa específica e do peso atômico. Com isso, testaremos as correlações conhecidas entre a aresta da célula unitária a e o raio atômico r   pra cada estrutura para averiguar qual é a mais apropriada!

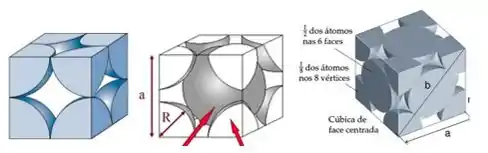
Na figura da esquerda, temos uma estrutura cúbica simples (CS), onde a = 2 r .Na figura do meio, temos uma estrutura cúbica de corpo centrado (CCC), onde 4 r = a 3 .

Na figura da direita, temos uma estrutura cúbica de face centrada (CFC), onde 4 r = a 2 .

Passo 2

Começando pela liga A, precisaremos calcular a massa dentro das células unitárias. Pra isso vamos usar a relação de Avogadro que diz que em 1 mol de moléculas existem 6,023   x   10 23 partículas! 77,4   g m o l ÷ 6,023   x   10 23 p a r t í c u l a s m o l = 77,4 g m o l x 1 6,023   x   10 23 m o l p a r t í c u l a s

1   p a r t í c u l a = 12,85   x   10 - 23 g   Pra estrutura CS, com 1 átomo por célula unitária, vamos ter uma massa total de : m C S = 12,85   x   10 - 23 g

Pra estrutura CCC, com 2 átomos, vamos ter uma massa total de : m C C C = 25,7   x   10 - 23 g

Pra estrutura CFC, com 4 átomos, vamos ter uma massa total de : m C F C = 51,4   x   10 - 23 g

Agora vamos calcular o volume!

Passo 3

Na estrutura CS, temos que: 2 r = a

Como temos que o raio é r A = 0,125   n m , obtemos que a = 0,250   n m

Calculando então o volume do cubo, temos que V C S A = a 3 = 0,015   n m ³ Na estrutura CCC, temos que: 4 r = a 3

Como temos que o raio é r A = 0,125   n m , obtemos que a = 0,289   n m

Calculando então o volume do cubo, temos que V C C C A = a 3 = 0,024   n m ³ Na estrutura CFC: 4 r = a 2

Como temos que o raio é r = 0,125   n m , obtemos que a = 0,354   n m

Calculando então o volume do cubo, temos que V C F C A = 0,044   n m ³

Passo 4

Finalmente, pra calcularmos a massa específica, precisamos tirar a razão entre a massa e o volume da célula unitária. Sem esquecer de fazer as devidas conversões de unidade! 1   n m = 10 - 7 c m Pra estrutura CS: ρ C C C =   m V =   12,85     x 10 - 23 0,015         x   10 - 21     = 8,57   g / c m ³ Pra estrutura CCC: ρ C C C =   m V =   25,7   x 10 - 23 0,024       x   10 - 21     = 10,71   g / c m ³ Pra estrutura CFC:

ρ C F C =   m V =   51,4   x 10 - 23 0,044   x   10 - 21     = 11,68   g / c m ³ Avaliando os valores encontrados, podemos deduzir que a liga A tem estrutura cúbica simples!

Passo 5

Fazendo um procedimento análogo para a liga B, obtemos as seguintes massas específicas:

ρ C S B = 9,49   g / c m 3 ρ C C C B = 12,33   g / c m 3 ρ C F C B = 13,42   g / c m ³

Avaliando os valores encontrados, podemos deduzir que a liga B tem estrutura cúbica de face centrada!Agora para a liga C! ρ C S C = 9,23   g / c m 3 ρ C C C C = 11,98   g / c m 3 ρ C F C C = 13,05   g / c m ³ Avaliando os valores encontrados, podemos deduzir que a liga c tem estrutura cúbica simples!

Resposta

Liga A – Estrutura CS

Liga B – Estrutura CFC

Liga C – Estrutura CS

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O iodo possui uma célula unitária ortorrômbica para a qual os parâmetros a, b e c da rede são 0,479; 0,725 e 0,978 nm, respectivamente.Se o fator de empacotamento atômico e o raio atômico valem 0,547
O ródio possui um raio atômico de 0,1345n m e uma massa específica de 12,41g / c m ³ ³. Determine se ele possui uma estrutura cristalina CFC ou CCC.
Calcule o fator de empacotamento atômico para a estrutura cristalina cúbica do diamante (Figura 12.15). Considere que os átomos tocam uns nos outros, que o ângulo entre ligações adjacentes é de 109.5º
O sulfeto de cádmio (CDS) apresenta uma célula unitária cúbica e, a partir de dados de difração de raios X, sabe-se que o comprimento da aresta da célula unitária é de 0,582 nm. Se a massa específica
Usando os raios iônicos da Tabela 12.3, calcule a massa específica teórica do CsCl. (Sugestão: use uma modificação do resultado do Problema 3.3).A massa específica medida é de 3.99 g / c m 3 . Como vo