A resistência ao desgaste de um eixo de aço deve ser aumentada, pelo endurecimento da sua superfície. Isto deve ser realizado pelo aumento do teor de nitrogênio na camada superficial mais externa como resultado da difusão de nitrogênio no aço. O nitrogênio deve ser fornecido a partir de um gás externo rico em nitrogênio a uma temperatura elevada e constante. O teor inicial de nitrogênio no aço é de 0,002% p, enquanto a concentração na superfície deve ser mantido a 0,50% p. Para que este tratamento seja efetivo, um teor de nitrogênio de 0,10% p deve ser estabelecido em uma posição 0,40 mm abaixo da superfície. Especifique tratamentos térmicos apropriados em termos da temperatura 475 ° C e 625 ° C. Ao longo dessa faixa de temperatura, a constante pré exponencial e a energia ativação para a difusão de nitrogênio no ferro são 3 × 10-7 m²/s e 76.150 J / mol, respectivamente.
Passo 1
Esta é uma situação de difusão em estado estacionário; Vamos considerar os dados dados no enunciado:
C0 = 0.002 wt% N
Cs = 0.50 wt% N
Cx = 0.10 wt% N
E aplicar na fórmula:
Agora, devemos usar as informações da Tabela 5.1
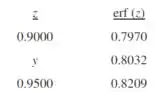
Vamos fazer interpolação para encontrar o valor de :
Resolvendo para , teremos:
Passo 2
Como , temos que achar a partir da equação:
Isolando D:
Passo 3
O coeficiente de difusão depende da temperatura de acordo com a expressão abaixo e temos que: e .
Dt
Isolando “t” em função de T temos:
Passo 4
Com a equação obtida no passo 3:
Devemos atribuir valores a dentro da faixa de valores citadas no enunciado (475 ° C a 625°C), para isso basta aplicarmos na equação:
OBS: todas as temperaturas deverão estar em K, então basta somar 273K
Para T = 480°C temos:
Para T = 550ºC temos:
Para T = 625ºC temos: