Enunciado
Ciência dos Materiais - Callister - Ciência e Engenharia de Materiais. Uma Introdução- Ed: 8º - Capítulo 6.Perguntas e Problemas - Ex. 2
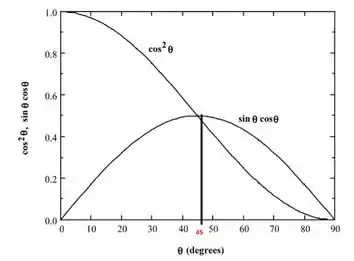
- As equações 6.4a e 6.4b são expressões para tensões normais (σ ′) e de cisalhamento (τ ′), respectivamente, em função da tensão de tração aplicada (σ) e do ângulo de inclinação do plano no qual essas tensões são realizadas (θ da Figura 6.4). Faça um gráfico no qual são apresentados os parâmetros de orientação dessas expressões (isto é, cos²θ e sin θ cos θ) em função de θ.
- A partir desse gráfico, em que ângulo de inclinação a tensão normal é máxima?
- Ainda, em que ângulo de inclinação a tensão de cisalhante é máxima?
Passo 1
- Para desenvolvermos o gráfico temos que definir as equações:
- A tensão máxima ocorre em um ângulo de inclinação de 0 °.
- A tensão máxima de cisalhamento ocorre em um ângulo de inclinação de 45 °.
e
O gráfico de cos² tem esse comportamento:
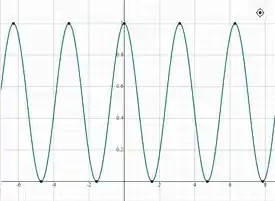
Para temos:
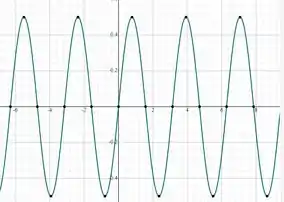
Então basta unirmos os gráficos para ver o comportamento:
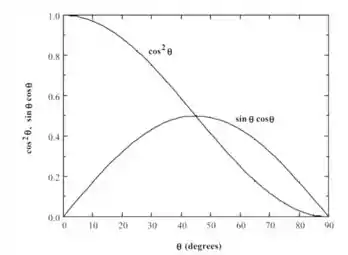
Passo 2
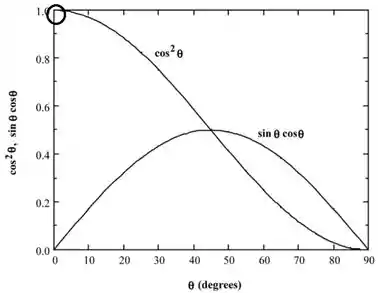
Passo 3
Resposta
- O°
- 45°
Exercícios de Livros Relacionados
Demonstre que a Equação 6.16, a expressão que define a deformação verdadeira, também pode ser representada por: ϵ V = l n A 0 A i quando o volume do corpo de provas permanece constante durante a defor
Um ensaio de tração é realizado em um corpo de provas metálico e determina-se que uma deformação plástica verdadeira de 0.20 é produzida quando uma tensão verdadeira de 575MPa (83500psi) é aplicada; p
Para uma dada liga metálica, uma tensão verdadeira de 415MPa (60175psi) produz uma deformação plástica verdadeira de 0.475. Se o comprimento original de um corpo de provas desse material é 300mm (11.8
Para um latão, as seguintes tensões verdadeiras produzem as deformações plásticas verdadeiras correspondentes:Qual é a tensão verdadeira necessária para produzir uma deformação plástica verdadeira de
Um latão, a ser usado como mola, deve possuir um módulo de resiliência de pelo menos 0,75 MPa(110 psi). Qual deve ser o seu limite de escoamento mínimo?