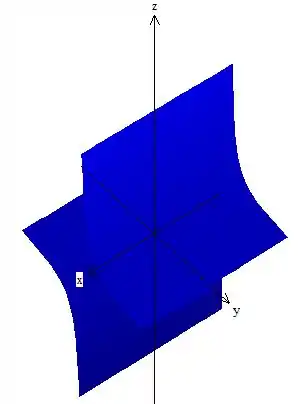
Esboce o cilindro:
Passo 1
Encontrar a curva diretriz e o eixo do cilindro.
A curva diretriz do cilindo é a curva , portante a variável irrestrita é e o eixo do cilindro é o eixo .
Passo 2
Agora vamos desenhar a curva , no plano
; ; ;
Portanto temos:
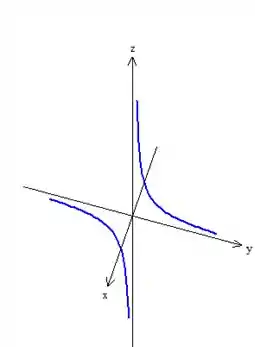
Passo 3
“Expandindo” a curva na direção do eixo do cilindro temos:

Resposta