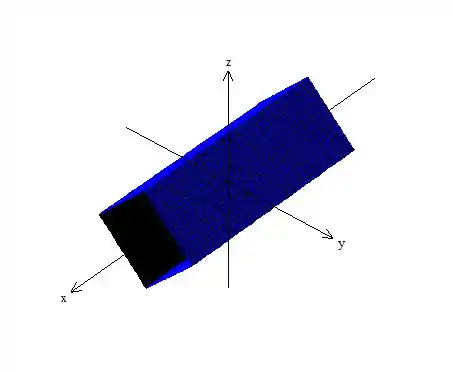
Faça um esboço do cilindro de equação dada.
Passo 1
Precisamos identifica a curva geratriz e o eixo do cilindro para fazer seu esboço. O eixo do cilindro é o eixo , é o eixo da variável livre, que não aparece na equação. Mas e a curva diretriz ???
Essa curva é um pouco mais complicada, vamos focar um pouco pra entender isso.
Quando temos módulo temos uma situação para o cara positivo e uma situação para o cara negativo.
Vamos considerar primeiro
Isso nos diz que
A função vai ser
O gráfico fica
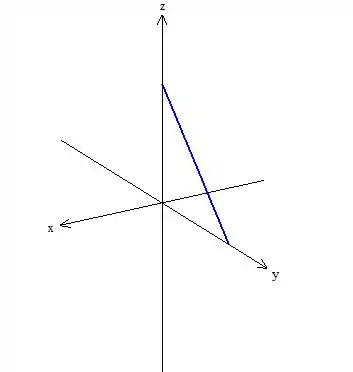
Passo 2
Vamos ver agora
Isso nos diz que
A função vai ser
O gráfico fica
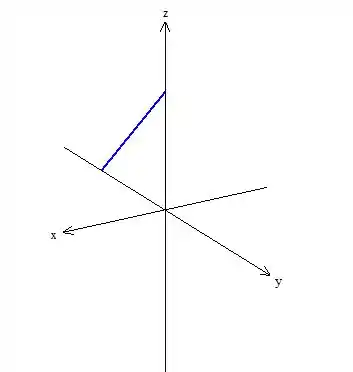
Passo 3
Vamos ver agora
Isso nos diz que
A função vai ser
O gráfico fica
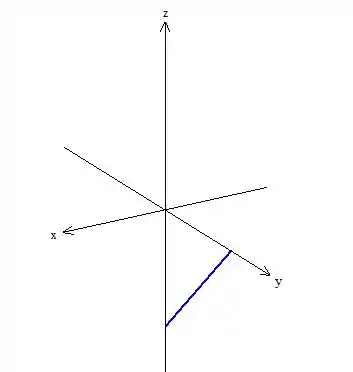
Passo 4
Vamos ver agora
Isso nos diz que
A função vai ser
O gráfico fica
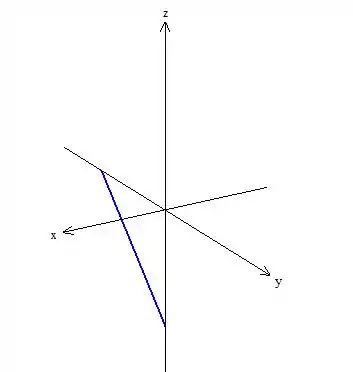
Passo 5
Juntando essa bagaça toda, vai ficar:
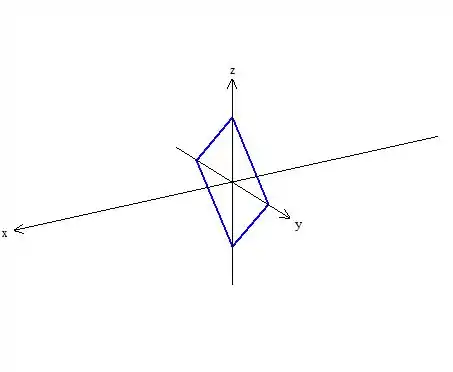
Essa é a nossa curva diretriz do cilindro!!!
Passo 6
Agora devemos desenhar novamente a curva geratriz: Uma mais a frente, representando os valores positivos e outra mais atrás representando so valores negativos. Fica assim:

Passo 7
Desenhando as diretrizes do cilindro temos:
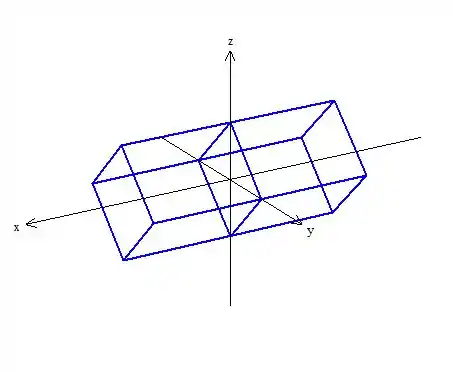
Passo 8
Finalmente, hachurando a superfície temos:
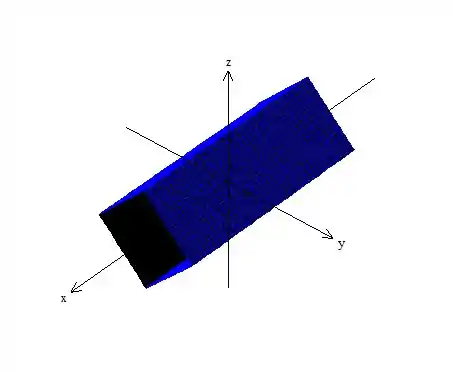
Resposta