Uma mistura de contendo molar de metanol em água devem ser separados por uma coluna de retificação em batelada. Para isso, uma coluna com 1 prato e condensador total é colocada sobre o ebulidor contendoa mistura e operada com uma razão de refluxo constante e igual a 2, à pressão atmosférica. A destilação é realizada até que da carga inicial tenham sido evaporados. Calcule a concentração final do resíduo.
![]()
Passo 1
A questão nos pede a concentração final do resíduo, mas para isso nós precisamos chutar um valor inicial e realizar diversas iterações até o valor convergir, beleza? Então vamos utilizar a expressão dada sabendo que .
Passo 2
Repara que tanto como são valores já fornecidos, então, podemos calcular o valor da fração:
Para toda a tabela. Fazendo as contas individualmente ficamos com:
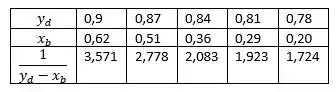
Nossa Júlia, mas porque você fez isso?? Para poder ficar mais fácil o nosso processo de iteração 😉
Passo 3
Antes de começar a iteração precisamos chutar um valor para o , eu vou começar pelo final da tabela mas você pode escolher qualquer um, ta bem? Então vamos lá, com , tenho:
Como a integral resultou em um valor maior que devemos chutar um valor de mais alto que . Então para o próximo chuto vamos pegar o penúltimo valor, .
Repara que não precisamos calcular a integral desde o começo pois podemos aproveitar o intervalo da primeira tentativa. Como o valor ainda é maior que devemos chutar um valor de .
O valor não é exatamente igual a mas repara que é bem mais próximo do que a nossa primeira integral. E como essa é uma conta muito braçal, normalmente o professor costuma pedir apenas três iterações. Sendo assim, fechamos com o .