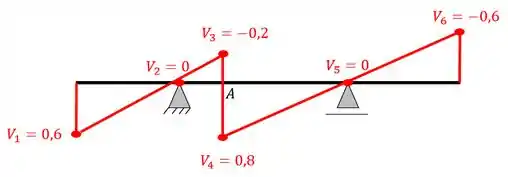
Determine a linha de influência de cortantes da seção A abaixo pelo método da carga unitária.
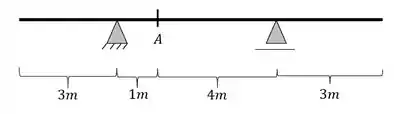
Passo 1
Sabemos que temos sempre que seguir um passo a passo para solucionar o nosso problema, e nesse caso o nosso passo a passo será:
- Primeiro devemos separar pontos chaves para calcularmos o valor do nosso cortante na seção A. Devemos lembrar que pontos chaves são extremidades, apoios, meios de vão, e outros pontos que devemos considerar de suma importância.
- Em seguida, em cada ponto chave colocamos a carga unitária, claro, lembrando de fazer uma de cada vez, e com a carga unitária posicionada calculamos as reações de apoio e cortantes na seção A.
- Por fim, teremos uma sequência de valores de cortante para nossa seção A, marcamos esses pontos na nossa viga e ligamos eles através de retas. Feito isso teremos exatamente a nossa linha de influência.
Entendido o processo de construção, vamos colocá-lo em pratica.
Passo 2
Como vimos, a primeira coisa que devemos fazer é marcar os pontos chaves de cálculo da nossa viga. Sabemos que devemos marcar esses pontos chaves da seguinte maneira
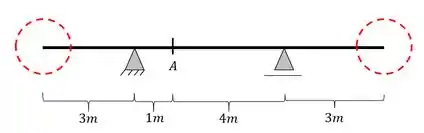
- Extremidades
- Apoios
- Seção Calculada (Direita/ Esquerda)
- Cortante na seção A devido a carga unitária na extremidade mais a esquerda
- Cortante na seção A devido a carga unitária no apoio mais á esquerda
- Cortante na seção A devido a carga unitária à esquerda da seção A
- Cortante na seção A devido a carga unitária à direita da seção A
- Cortante na seção A devido a carga unitária no apoio mais a direita
- Cortante na seção A devido a carga unitária na extremidade mais a Direita
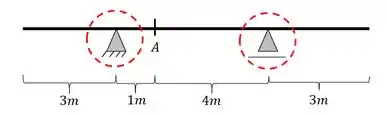
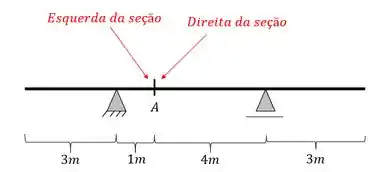
feito isso vamos ao próximo passo.
Passo 3
Esse passo se refere ao cálculo do cortante na seção A. Sabemos que em cada ponto chave do passo anterior devemos colocar uma carga unitária. Dessa forma teremos os seguintes valores de cortantes na nossa seção A da viga.
Primeiro colocamos a nossa carga unitária posicionada
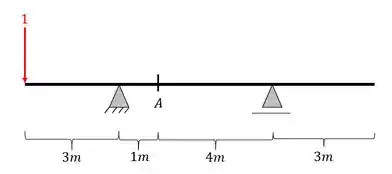
Depois calculamos as reações de apoio da nossa viga
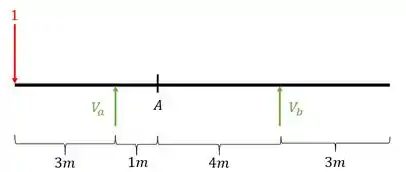
Usando as fórmulas de equilíbrio teremos que
Como deu negativo basta invertermos o nosso vetor
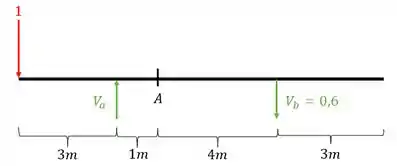
Calculando teremos que
Cortando a parte esquerda da nossa viga na seção A teremos que
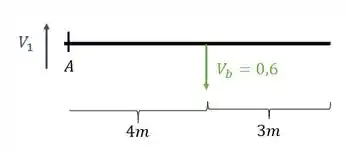
Logo o cortante que equilibra a viga será
Positivo pois sabemos que quando estamos vindo pela esquerda com vetor cortante pra cima o sinal no nosso cortante é positivo. Com isso calculamos o valor do nosso cortante na seção A quando temos uma carga unitária na extremidade. Vamos ao próximo ponto chave.
Passo 4
Primeiro colocamos a nossa carga unitária posicionada
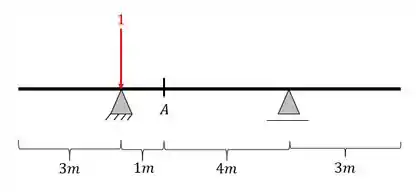
Depois calculamos as reações de apoio da nossa viga
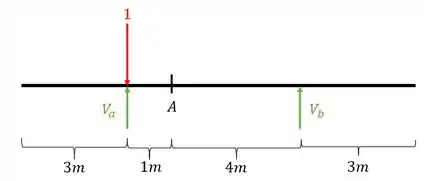
Usando as fórmulas de equilíbrio teremos que
Logo para teremos que
Cortando a parte esquerda da nossa viga na seção A teremos que
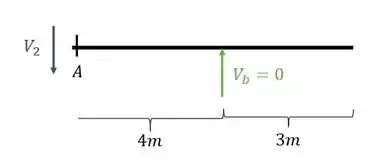
Logo o cortante que equilibra a viga será
Com isso calculamos o valor do nosso cortante na seção A quando temos uma carga unitária no apoio mais à esquerda. Vamos ao próximo ponto chave.
Passo 5
Primeiro colocamos a nossa carga unitária posicionada
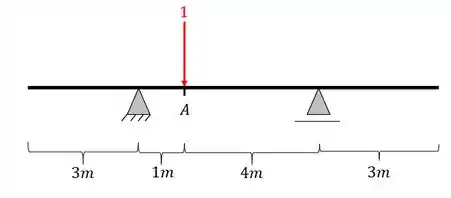
Depois calculamos as reações de apoio da nossa viga
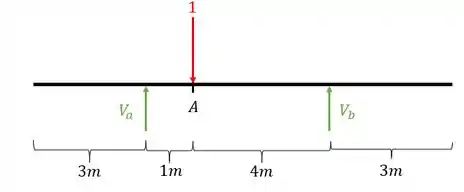
Usando as fórmulas de equilíbrio teremos que
Logo para teremos que
Cortando a parte esquerda da nossa viga na seção A, e lembrando que nesse caso a nossa carga esta um pouquinho para esquerda, o que fará ela sumir, teremos que
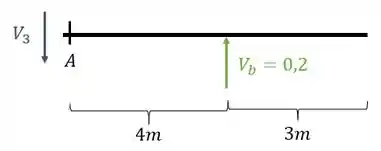
Logo o cortante que equilibra a viga será
É negativo nesse caso porque vindo pela esquerda o nosso cortante está para baixo, o que caracteriza ele como um cortante negativo. Com isso calculamos o valor do nosso cortante na seção A quando temos uma carga unitária na seção A mais à esquerda. Vamos ao próximo ponto chave.
Passo 6
Primeiro colocamos a nossa carga unitária posicionada
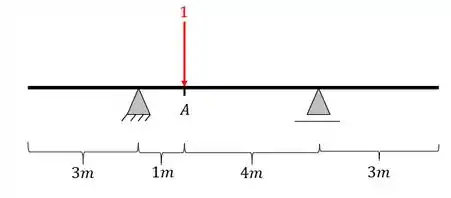
Depois calculamos as reações de apoio da nossa viga
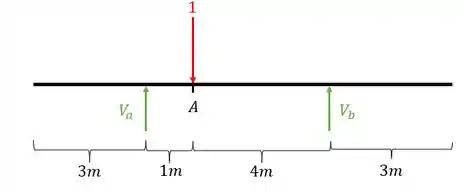
Usando as fórmulas de equilíbrio teremos que
Logo para teremos que
Cortando a parte esquerda da nossa viga na seção A, e lembrando que nesse caso a nossa carga está um pouquinho para direita, o mantém ela, teremos que
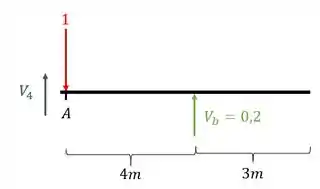
Logo o cortante que equilibra a viga será
Positivo pois sabemos que quando estamos vindo pela esquerda com vetor cortante pra cima o sinal no nosso cortante é positivo. Com isso calculamos o valor do nosso cortante na seção A quando temos uma carga unitária a direita da seção A. Vamos ao próximo ponto chave.
Passo 7
Primeiro colocamos a nossa carga unitária posicionada
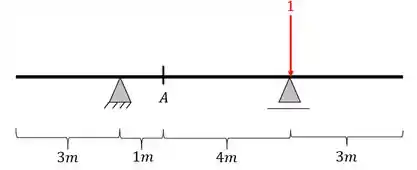
Depois calculamos as reações de apoio da nossa viga
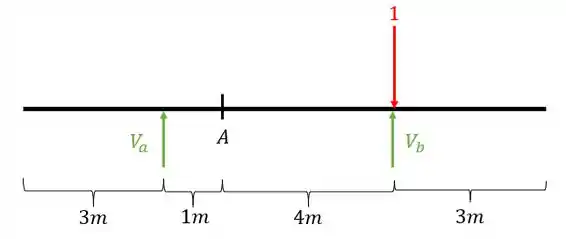
Usando as fórmulas de equilíbrio teremos que
Logo para teremos que
Cortando a parte esquerda da nossa viga na seção A teremos que
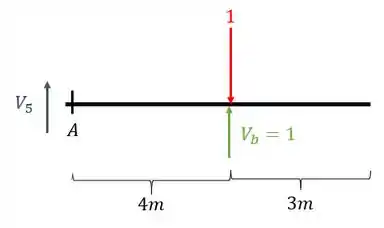
Logo o cortante que equilibra a viga será
Com isso calculamos o valor do nosso cortante na seção A quando temos uma carga unitária no apoio mais à direita. Vamos ao próximo ponto chave.
Passo 8
Primeiro colocamos a nossa carga unitária posicionada
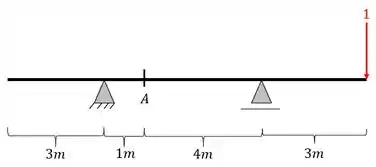
Depois calculamos as reações de apoio da nossa viga
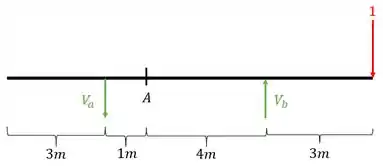
Usando as fórmulas de equilíbrio teremos que
Calculando teremos que
Cortando a parte esquerda da nossa viga na seção A teremos que
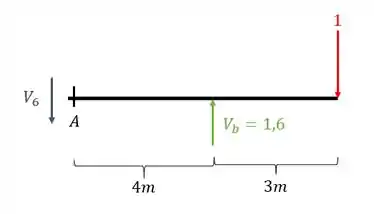
Logo o cortante que equilibra a viga será
Apesar de matematicamente o valor ser positivo, ele aparece como negativo pois sempre que o nosso cortante vem para baixo pela esquerda seu sinal é negativo, por isso, temos que nesse caso o nosso cortante é negativo. Com isso calculamos o valor do nosso cortante na seção A quando temos uma carga unitária na extremidade.
Passo 3
Vemos que depois de calcularmos os pontos chaves, devemos marca-los na viga e ligarmos os pontos através de retas, dessa forma teremos que
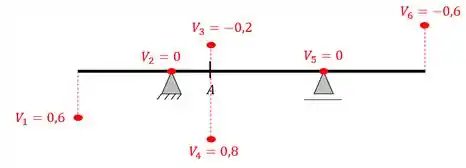
Perceba que na linha de influência, os valores positivos ficam na parte de baixo e os negativos na parte de cima. Alguns professores usam os sinais normais (positivo em cima e negativo em baixo) mas a maioria dos livros usam o esquema de sinais mostrados acima, mas os sinais não têm importância se você sempre usar a mesma regra, basta apenas não misturar.
Com isso, ligando os pontos, a nossa linha de influência será.
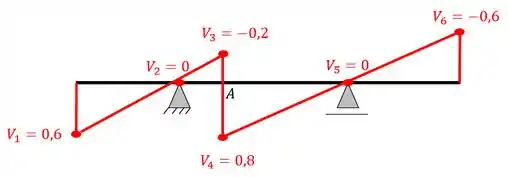
Resposta
Linha de influência de cortantes na seção A