Use o critério de Nyquist para determinar a estabilidade de um sistema com realimentação unitária e função de transferência mostrada abaixo:

Devemos agora esboçar o diagrama de Nyquist variando o valor de de até . Usando um software conseguimos a seguinte imagem:

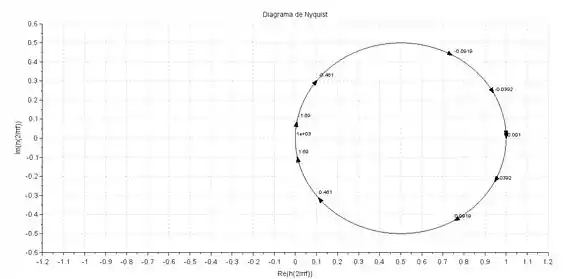
Os números ao longo da curva são referentes à frequência em que a função de transferência está sendo mapeada.

Repare que em o diagrama tende a , e quando tende a o diagrama tende a zero, uma vez que o denominador será muito maior que o denominador da função de transferência.

Além disso, o diagram chega em , formando um ângulo de . Isso acontece porque temos um polo a mais que zero nessa função de transferência.

Para determinar se o sistema é estável ou não, devemos determinar o número de raízes da equação característica em malha fechada no semiplano direito através da fórmula abaixo:

Onde, é o número de raízes positivas da equação características, é o número de voltas que o diagrama dá em , e é o número de polos positivos em malha aberta. Para que o sistema seja estável não pode haver rízes positivas da equação característica, ou seja, .

Para este exemplo, porque o diagrama não circula , e o único polo que existe em malha aberta é , logo, .

Sendo asism:

O sistema é estável.