Use o critério de Nyquist para determinar a estabilidade de um sistema com realimentação unitária e função de transferência mostrada abaixo:
Passo 1
Primeriamente precisamos fazer o esboço do diagrama de Nyquist para a função de transferência. Para isso, substituímos por e varíamos de ate´.
Substituindo por :
Passo 2
Devemos agora esboçar o diagrama de Nyquist variando o valor de de até . Usando um software, o diagrama de Nyquist é dado na figura abaixo:
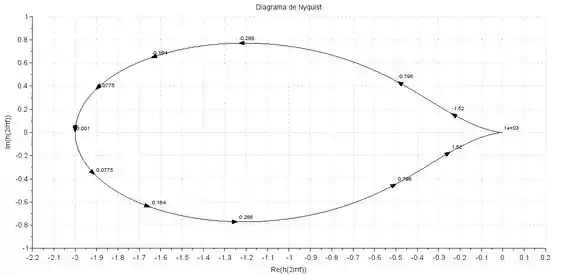
Em o diagrama tende a , e quando assume valores muito altos o diagarama de Nyquist vai para .
Além disso, podemos perceber em frequências altas, o ângulo de fase é , já que existem dois polos a mais que zeros.
Passo 3
Para determinar se o sistema é estável ou não, devemos determinar o número de raízes da equação característica em malha fechada no semiplano direito através da fórmula abaixo:
Onde, é o número de raízes positivas da equação características, é o número de voltas que o diagrama dá em , e é o número de polos positivos em malha aberta. Para que o sistema seja estável não pode haver rízes positivas da equação característica, ou seja, .
Para este exemplo, porque o diagrama dá uma volta em no sentido antihorário, e existe um polo positivo em malha aberta, , logo, .
Sendo asism:
O sistema é estável.
Resposta
Sistema estável