Elabore uma função recursiva capaz de realizar o cálculo de uma multiplicação recebendo como parâmetro dois números inteiros e positivos.
Passo 1
Transferindo todas as informações do enunciado para o escopo de uma função chamada temos o seguinte trecho de código:
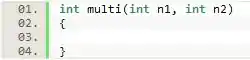
Uma função com tipo de retorno int que espera como parâmetro dois números e também inteiros.
Passo 2
Agora que já sabemos as entradas e saídas esperadas da nossa função, podemos definir o caso básico que ela terá.
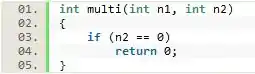
Nesse caso, utilizaremos a condição para impedirmos a criação de novas instâncias recursivas (o motivo disso vai ficar mais óbvio no próximo passo).
Passo 3
A grande sacada para calcular uma multiplicação através de uma função recursiva está na realização de múltiplas somas.
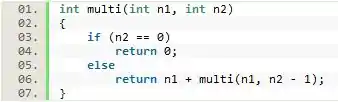
Por esse motivo podemos somar o valor de e chamar recursivamente a função passando como parâmetro o próprio e . Isso fará com que seja um contador das somas de (por isso o caso básico retorna nas instâncias recursivas quando ) fazendo com que seja somado com ele mesmo vezes, resultando assim em .
Resposta
Ei, a resposta está no passo a passo :)