Seja o somatório abaixo. Faça uma função recursiva para realizar o cálculo.
Passo 1
Sempre quando vamos criar uma função recursiva nós temos que ter uma visão geral dela, para isso devemos primeiro declarar o seu escopo.
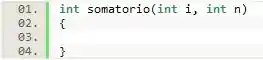
Como o somatório gerará um resultado inteiro, o tipo de retorno dessa função chamada deve ser int. Além disso, essa função deve esperar como parâmetros o valor inicial (que pelo somatório do enunciado é dado como 1) e o limite superior .
Passo 2
Tendo em vista o escopo dessa função podemos agora definir o caso básico.
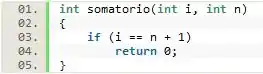
A lógica desse caso básico consistem em parar o somatório uma unidade depois de que é o limite superior (e deve ser calculado). Nesse caso, a forma de parar e retornar nas instâncias criadas é retornar o valor 0 (que é nulo em uma soma).
Passo 3
Por fim, basta criarmos a regra de criação de instâncias (que praticamente é dada no enunciado).
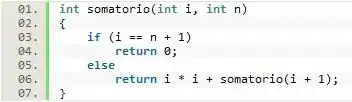
Basicamente o que nós fazemos é calcular o quadrado de e chamar recursivamente passando como parâmetro a própria função. Isso fará com que quando o caso básico seja verdadeiro, essas instâncias comecem a retornar os resultados dos até que por último o primeiro quadrado de seja somado com a soma de todos os quadrados seguintes até .
Resposta
Isso pode parecer muito complicado, mas recursão é isso. Você avança em instâncias até o caso básico ser verdadeiros depois elas começar a retornar resultados que em conjunto resolvem o problema geral. Nesse caso, o somatório.