O máximo divisor comum (MDC) de dois números inteiros e pode ser calculado usando-se uma definição recursiva:
Além disso, sabe-se que:
Passo 1
Vamos lá, a primeira coisa que nós temos que fazer para criarmos essa função é definir o escopo da nossa função.
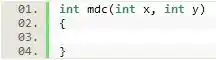
Com isso, sabemos que se trata de uma função com retorno de valor inteiro (o M.D.C) chamada que recebe como parâmetros dois números inteiros e como parâmetro.
Passo 2
Agora que já temos uma visão geral da nossa função, podemos definir o caso básico que limitará as chamadas recursivas.
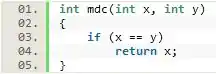
Um aspecto super interessante desse exercício é que podemos utilizar como caso básico uma das propriedades dadas no enunciado, que é . No caso, se durante as instâncias da recursão obtermos igual a , basta retornamos como máximo divisor comum.
Passo 3
Com o nosso caso básico prontinho, podemos definir a regra que irá criar as instâncias recursivas.
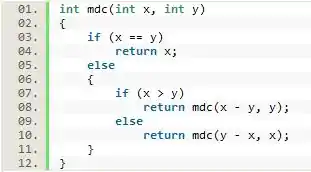
Basicamente nós simplesmente temos que fazer a verificação de é maior que . Caso seja, utilizamos a regra , caso contrário, temos que utilizar a regra . Utilizando essa regra de criação de instância, chegaremos em um momento em que , ou seja, temos o valor do máximo divisor comum.
Resposta
Ei, a resposta está no passo a passo :)