Elabore uma função recursiva que dado um número retorne o n-ésimo termo da sequência de Fibonacci. Considere a seguinte sequência:
Passo 1
Para iniciarmos o desenvolvimento da nossa função, temos que primeiro definirmos o seu escopo.
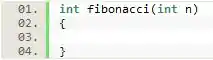
Para isso, como se trata de uma função que retorna o n-ésimo termo da sequência de Fibonacci, o tipo de retorna da função chamada deve ser int. Além disso, ela espera como parâmetro um número também inteiro.
Passo 2
Agora que já temos uma visão geral da nossa função, podemos definir o caso básico dela.
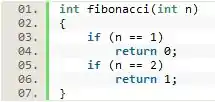
Esse caso básico não se trata de um limitador de criação de instâncias recursivas, mas sim de uma solução para o caso em que a entrada é o primeiro ou segundo termo da sequência. Isso acontece, pois esses termos não são calculados e servem como base para o cálculo da sequência já que o n-ésimo termo é a soma entre os termos e .
Passo 3
Por fim, agora que já temos um contorno para os dois primeiros termos, podemos criar uma regra de chamadas recursivas para o cálculo de qualquer termo da sequência.
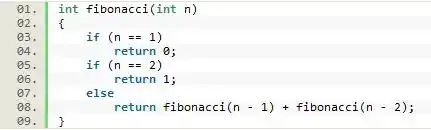
Essa regra nada mais é do que se chamar recursivamente para calcular o valor da sequência dos dois termos anteriores a ( e ) e retornar a soma entre eles (já que ), obtendo assim o n-ésimo valor da sequência de Fibonacci.
Resposta
Ei, a resposta está no passo a passo :)