Uma torre de fracionamento deve ser projetada para processar uma mistura com , líquida saturada. Determine a razão de refluxo sabendo:
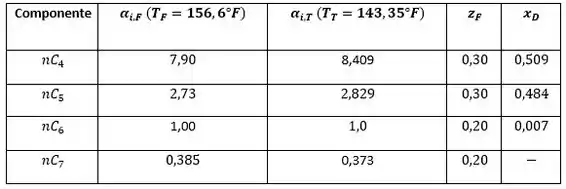
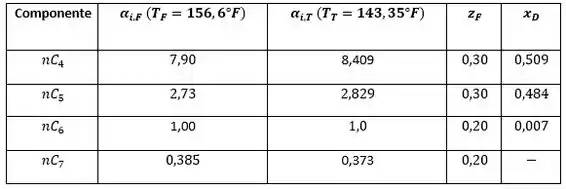
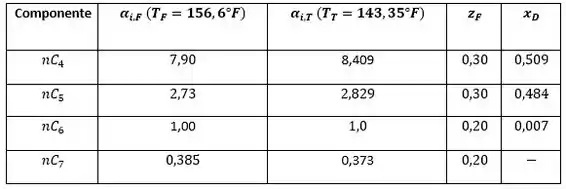
Dado:
Passo 1
Faaala aí, tudo certinho? Nessa questão nós precisamos encontrar o valor da razão de refluxo. Entãaao, vamos usar a equação de Underwood. Primeiro calculando o valor de para depois calcular a razão de refluxo mínimo e por último a razão de refluxo.
Passo 2
A questão nos diz que estamos trabalho com uma mistura líquida saturada, ou seja,
E como,
Passo 3
Agora que já temos o valor de , podemos substituir os valores da tabela com o valor de do fundo da coluna,
Na primeira equação para encontrar o :
Fazendo as contas encontramos, (lembrando que )
Passo 4
Já com o valor de vamos agora encontrar a razão de refluxo mínima com,
Substituindo o valor de calculado e os valores da tabela com o do topo da coluna,
Fazendo as contas encontramos,
Passo 5
Agora podemos finalmente calcular a razão de refluxo,
Lembrando que o enunciado nos deu,
Logo,