Superposição, Thévenin e Norton para Corrente Alternada
Teoria
Nesse tópico vamos ver como funcionam as técnicas de Superposição, Circuito equivalente de Thévenin e Norton para CA. Você vai ver que esses métodos serão executados de maneira igual a quando estudamos circuitos CC.
Superposição
O teorema da superposição também pode ser aplicado em circuitos CA, pois, assim como os circuitos CC, eles são lineares. O procedimento é exatamente o mesmo: calcular a contribuição de cada fonte e depois somar.
Além disso, esse teorema é muito importante para o caso de um circuito possuir fontes com frequências diferentes. Nesse caso, para cada frequência teremos um circuito no domínio da frequência.
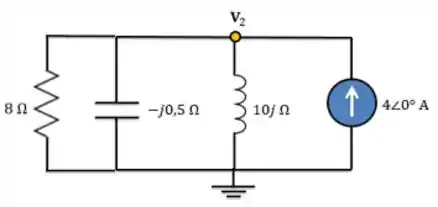
Vamos fazer um exemplo para você entender melhor. No circuito abaixo, vamos calcular usando o teorema da superposição:
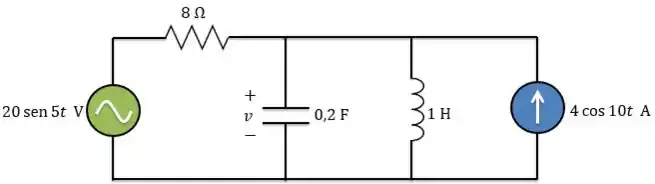
Passo 1:
Aplicando o princípio da superposição, a tensão será dada por:
Onde é a contribuição da fonte de tensão e é a contribuição da fonte de corrente.
Passo 2:
Para determinar , temos que desligar a fonte de corrente, ou seja, considerá-la um circuito aberto e passar o circuito para o domínio da frequência.
Logo, o circuito no domínio da frequência é:
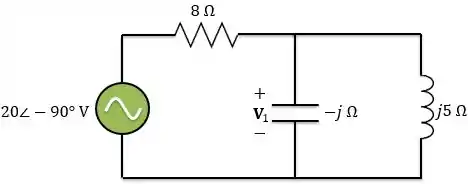
Passo 3:
Agora, vamos utilizar a análise nodal:
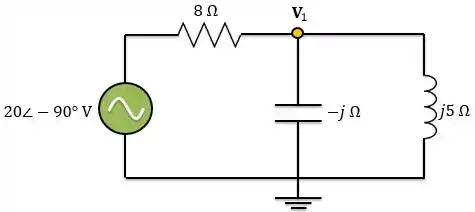
Aplicando a LCK ao nó:
Voltando para o domínio do tempo:
Passo 4:
Para determinar , temos que desligar a fonte de tensão, ou seja, considerá-la um curto-circuito e passar o circuito para o domínio da frequência.
Logo, o circuito no domínio da frequência é:
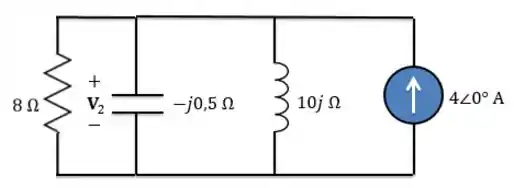
Passo 5:
Para encontrarmos , vamos utilizar análise nodal mais uma vez.
Aplicando a LCK ao nó:
Voltando para o domínio do tempo:
Passo 6:
Logo, pelo princípio da superposição, a tensão é dada por:
Pronto! Missão cumprida!
Transformação de fontes
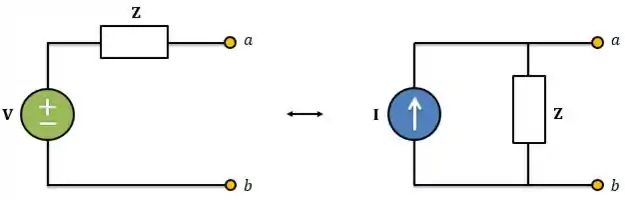
Lembra de transformação de fontes? Para circuitos CA ela também é válida. Só que para esse caso, a transformação de fontes ocorre no domínio da frequência e significa transformar uma fonte de tensão em série com uma impedância em uma fonte de corrente em paralelo com a mesma impedância.
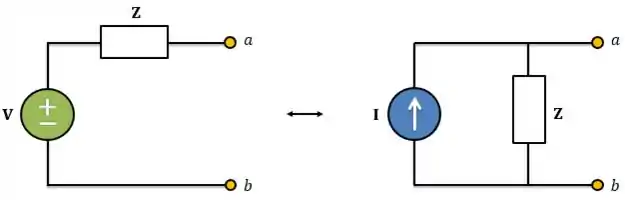
Sempre lembrando que a transformação tem que respeitar a lei de Ohm:
Teorema de Thévenin e Norton
Adivinha só! Esses teoremas também são válidos em circuitos CA. Além disso, eles são aplicados da mesma maneira que são aplicados em circuitos CC, só que no caso CA analisamos fasorialmente o circuito e os circuitos equivalentes são:
Circuito Equivalente de Thévenin:
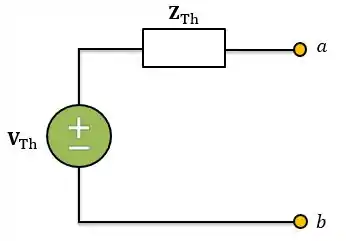
Circuito Equivalente de Norton:
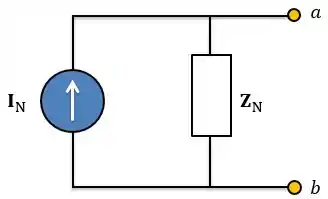
Lembrando que é tensão de circuito aberto, é a corrente de curto-circuito e é a impedância equivalente vista pelos terminais . Além disso, os circuitos equivalentes se relacionam como em uma transformação de fonte:
Para você relembrar como funciona esses teoremas, vamos fazer um exemplo. No circuito abaixo, vamos obter o circuito equivalente de Thévenin e Norton:
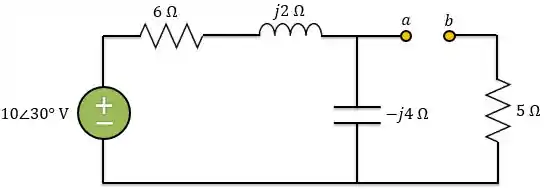
Passo 1:
Nosso primeiro passo é determinar a impedância de Thévenin . Para isso, desligamos a fonte independente e calculamos a impedância equivalente vista pelos terminais . Logo, analisando o circuito abaixo, temos:
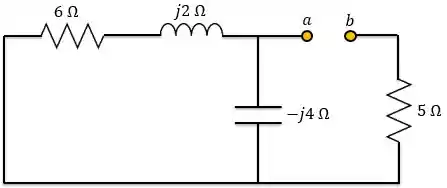
Passo 2:
Agora, precisamos encontrar a tensão de circuito aberto aplicada nos terminais Para isso, vamos analisar o circuito abaixo:
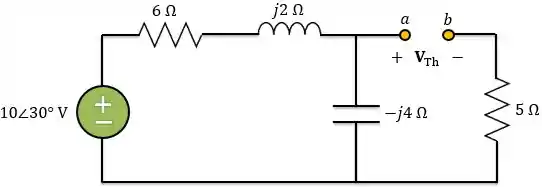
Como o circuito está aberto, não tem circulação de corrente pelo resistor de e, consequentemente, não há queda de tensão no mesmo. Portanto, podemos considerar o circuito abaixo:
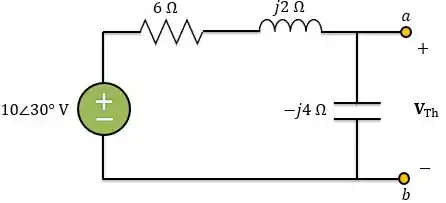
Aplicando divisor de tensão, temos:
Passo 3:
Logo, o circuito equivalente de Thévenin é:
Aplicando tranformação de fontes podemos obter o circuito equivalente de Norton:
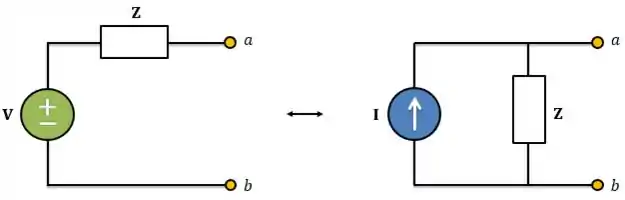
Pronto! Agora é partir para os exercícios!
Transformação de fontes
Teorema de Thévenin e Norton
Exercícios Resolvidos
Exercício Resolvido #1
Livro Sadiku, p.398, Problema 10.40
Determine no circuito abaixo usando superposição.
Passo 1
Aplicando o princípio da superposição, a corrente será dada por:
Onde é a contribuição da fonte de tensão alternada e é a contribuição da fonte de tensão CC.
Passo 2
Para determinar , temos que desligar a fonte de tensão CC, ou seja, considerá-la um curto-circuito e passar o circuito para o domínio da frequência.
Logo, o circuito no domínio da frequência é:
Passo 3
Agora, vamos utilizar a análise nodal:
Logo, pela lei de Ohm:
Voltando para o domínio do tempo:
Passo 4
Para determinar , temos que desligar a fonte de tensão CA, ou seja, considerá-la um curto-circuito e considerar apenas a fonte CC. Além disso, temos que lembrar que em regime permanente CC o indutor é um curto-circuito. Portanto, temos que analisar o seguinte circuito:
Toda a corrente fornecida pela fonte passa pelo curto-circuito. Logo, não tem circulação de corrente no resistor e será:
Passo 5
Logo, pelo princípio da superposição, a corrente é dada por:
Resposta
Exercício Resolvido #2
Livro Sadiku, p.398, Problema 10.46
Determine no circuito abaixo usando superposição.
Passo 1
Aplicando o princípio da superposição, a tensão será dada por:
Onde é a contribuição da fonte de tensão alternada, é a contribuição da fonte de corrente e da fonte de tensão CC.
Passo 2
Para determinar , temos que desligar a fonte de tensão CC e a fonte de corrente, ou seja, considerar a fonte CC um curto-circuito e a fonte de corrente um circuito aberto. Passando o circuito para o domínio da frequência, temos:
Logo, o circuito no domínio da frequência é:
Passo 3
Agora, vamos utilizar a análise nodal:
Aplicando a LCK ao nó:
Voltando para o domínio do tempo:
Passo 4
Para determinar , vamos considerar apenas a fonte de corrente. Portanto, substituindo as fontes de tensão por curtos-circuitos e passando o circuito para o domínio da frequência, temos:
Logo, o circuito no domínio da frequência é:
Passo 5
Agora, vamos utilizar a análise nodal mais uma vez:
Aplicando a LCK ao nó:
Voltando para o domínio do tempo:
Passo 6
Para terminar, precisamos calcular a contribuição da fonte de tensão CC. Desligando as outras fontes e lembrando que em regime permanente CC o capacitor é um circuito aberto e o indutor um curto-circuito, temos o circuito abaixo:
Logo,
Passo 7
Logo, pelo princípio da superposição, a tensão é dada por:
Resposta
Exercício Resolvido #3
Livro Sadiku, p.398, Problema 10.49
Usando a transformação de fontes, determine no circuito abaixo:
Passo 1
De cara, temos que passar o circuito para o domínio da frequência:
Portanto, o circuito no domínio da frequência será:
Passo 2
Agora, vamos utilizar transformação de fontes. Transformando a fonte de corrente em paralelo com o resistor de em uma fonte de tensão em série com o mesmo resistor, temos:
Passo 3
Portanto, a impedância do circuito é:
Aplicando a lei de Ohm encontramos a corrente:
Voltando para o domínio do tempo, temos:
Resposta
Exercício Resolvido #4
Livro Sadiku, p.398, Problema 10.52
Utilize o método da transformação de fontes para determinar no circuito abaixo:
Passo 1
O circuito já está na forma fasorial. Então, podemos partir direto para as transformações de fonte. Primeiro, vamos considerar:
Transformando a fonte de tensão em série com a impedância em uma fonte de corrente em paralelo com , temos que a fonte de corrente terá o seguinte valor:
Portanto, temos o seguinte circuito:
Passo 2
Considerando:
Usando mais uma vez transformação de fontes. Vamos transformar a fonte de corrente em paralelo com em uma fonte de tensão em série com . O valor da fonte de tensão será:
Portanto, o circuito fica assim:
Passo 3
Agora, vamos considerar:
Então, vamos transformar a fonte de tensão em série com em uma fonte de corrente em paralelo com . O valor da fonte de corrente será:
Logo, temos o seguinte circuito:
Passo 4
Para terminar, vamos aplicar divisor de corrente:
Resposta
Exercício Resolvido #5
Livro Sadiku, p.398, Problema 10.56
Para o circuito abaixo, obtenha os circuitos equivalentes de Thevenin e de Norton nos terminais .
Passo 1
O circuito já está no domínio da frequência. Além disso, se o analisarmos e o redesenharmos vemos que ele já pode ser considerado o circuito equivalente de Norton. Olha só:
Passo 2
Calculando a impedância de Norton, temos:
Passo 3
Logo, o circuito equivalente de Norton é:
Passo 4
Para encontrarmos o circuito equivalente de Thevenin basta utilizarmos transformação de fontes. Vamos transformar a fonte de corrente em paralelo com a impedância em uma fonte de tensão em série com a mesma impedância .
Logo, o circuito equivalente de Thévenin é:
Resposta
Exercício Resolvido #6
Livro Sadiku, p.398, Problema 10.55
Determine os circuitos equivalentes de Thévenin e de Norton nos terminais para o circuito abaixo:
Passo 1
Como o circuito já foi dado no domínio da frequência, o primeiro passo é calcular a impedância de Thévenin do circuito .
Para isso, desligamos a fonte independente do circuito e calculamos a impedância vista pelos terminais :
Passo 2
Para calcularmos a , fazemos:
Passo 3
Agora precisamos encontrar a tensão de circuito aberto entre os terminais .
Como o circuito está aberto, não passa corrente no resistor de e, portanto, não há queda de tensão nele. Por isso, o circuito fica como o da figura abaixo:
Logo, a tensão do circuito equivalente de Thévenin é a mesma do capacitor.
Passo 4
Para calcularmos a , utilizaremos divisor de tensão:
Passo 5
Logo, o circuito equivalente de Thévenin será:
Passo 6
Para encontrar o circuito equivalente de Norton, temos que utilizar a transformação de fontes. Então, respeitando a Lei de Ohm, teremos:
Lembrando que , o circuito equivalente de Norton será:
Resposta
Exercício Resolvido #7
Livro Sadiku, p.398, Problema 10.62
Usando o teorema de Thevenin, determine no circuito abaixo:
Passo 1
De cara, temos que passar o circuito para o domínio da frequência:
Portanto, o circuito no domínio da frequência será:
Passo 2
Agora, vamos aplicar o teorema de Thevenin para encontrar . Para isso, temos que retirar o resistor de e encontrar o circuito equivalente de Thevenin a esquerda dos terminais .
Passo 3
Agora, vamos calcular . O circuito tem uma fonte dependente de corrente, temos que lembrar que não desligamos fontes dependentes, apenas desligamos as independentes.
Além disso, para esse caso nós conectamos uma fonte de tensão nos terminais que fornece ao circuito uma corrente e encontramos através da relação abaixo:
Passo 4
Para encontrar vamos utilizar análise nodal no circuito abaixo:
Aplicando a LCK ao nó 1:
Pela lei de Ohm:
Substituindo:
Agora, vamos aplicar a LCK ao nó 2:
Substituindo e simplificando, temos:
Passo 5
Igualando as equações e , temos:
Agora, vamos simplificar:
Portando:
Passo 6
Agora precisamos encontrar que é a tensão de circuito aberto entre os terminais .
Para isso, vamos utilizar mais uma vez análise nodal.
Aplicando a LCK ao nó 1:
Nesse circuito:
Substituindo:
Agora, vamos aplicar a LCK ao nó 2:
Substituindo o valor e simplificando, temos:
Passo 7
Com as equações e chegamos ao sistema abaixo:
Isolando em :
Agora, substituindo em :
Passo 8
Agora que temos os valores de e podemos substituir todo o circuito a esquerda dos terminais pelo circuito equivalente de Thevenin.
Agora, vamos aplicar divisor de tensão para encontrarmos :
Para terminar, precisamos voltar para o domínio do tempo:
Resposta
Exercício Resolvido #8
Livro Sadiku, Problema 10.41
Determine no circuito da figura supondo que
Passo 1
Usando o princípio da superposição, vamos separar nossa tensão em duas partes e trabalhar com cada uma individualmente. Vamos lá.
Passo 2
Para , o será , então podemos calcular nossa reatância do capacitor
E daí, vamos desenhar o novo circuito
Usando divisor de tensão, vamos calcular nosso :
ou, no domínio do tempo:
Passo 3
Para , o será , então podemos calcular nossa reatância do capacitor
E daí, vamos desenhar o novo circuito
Usando divisor de tensão, vamos calcular nosso :
ou, no domínio do tempo:
Passo 4
Agora, usando o teorema da Superposição, vamos somar as duas tensões:
Resposta
Exercício Resolvido #9
Livro Sadiku, Problema 10.59
Calcule a impedância de saída do circuito mostrado na figura
Passo 1
Vamos começar colocando uma fonte de corrente de nos terminais desse circuito para podermos fazer a análise. Desse modo, chegaremos na figura abaixo:
Passo 2
A gente quer a impedância de saída, então pra isso, vamos calcular a tensão primeiro.
Bom, vamos começar pela tensão
(já que )
Agora vamos aplicar a Lei de Kirchhoff das correntes no nó :
(já que e
Passo 3
Agora, vamos aplicar a Lei das Malhas aqui:
Substituindo os valores que a gente encontrou antes… chegamos em:
Passo 4
Agora sim, podemos achar a impedância através da primeira Lei de Ohm:
Substituindo os valores encontrados anteriormente:
Resposta
Exercício Resolvido #10
Livro Sadiku, Problema 10.61
Determine o circuito equivalente de Thévenin nos terminais a-b do circuito da figura
Passo 1
Vamos começar desenhando todas as correntes e a tensão de Thévenin
Passo 2
E agora vamos aplicar a Lei das Correntes de Kirchhoff no nó para achar
Passo 3
E com isso podemos achar para então calcular
Substituindo o valor de
Passo 4
Usando a Primeira Lei de Ohm:
Substituindo os valores encontrados antes:
Passo 5
Vamos desenhar o circuito agora com uma fonte de corrente de entre os terminais a e b
Passo 6
Com essa fonte de corrente, podemos calcular a impedância de Thévenin
Substituindo os valores encontrados antes:
Vamos somar as nossas impedâncias e usar a Primeira Lei de Ohm:
Resposta
