Potência em Circuito CA
Produzido por Alexandre NunesTeoria
Demorou mas chegou a hora. Até agora não tínhamos estudado como funciona a potência em circuitos de corrente alternada. Nesse tópico vamos começar! Se segura aí e vem comigo!
Potência instantânea
A potência instantânea é a potência em qualquer instante e nada mais é do que o produto da tensão instantânea e a corrente instantânea .
Então, supondo que e , vamos calcular a potência instantânea.
Lembrando da identidade trigonométrica
Temos:
Lembrando que a sua unidade é watts .
Como podemos notar, a potência instantânea tem uma parcela constante que depende da diferença de fase entre a tensão e a corrente e a outra parcela é uma função senoidal que possui o dobro da frequência angular. Vou escrever a forma generalizada para você visualizar.
Sendo,
A potência instantânea é
Potência média
Como a potência instantânea varia com o tempo, fica difícil dela ser medida. Mas com um instrumento chamado wattímetro podemos medir a potência média, que é a média da potência instantânea.
A sua definição é
Mas para evitar de ficar calculando integral eu vou te dar uma dica: a potência média é igual a parcela constante da potência instantânea, ou seja:
Lembrando essa fórmula não tem erro!
Partiu fazer um exemplo! No circuito abaixo vamos calcular a potência média fornecida pela fonte e a potência média absorvida pelo resistor.
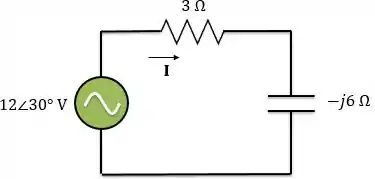
Nosso primeiro passo é encontrar a corrente :
Agora que temos a tensão e a corrente , vamos calcular a potência média fornecida pela fonte:
Agora, vamos calcular a potência média absorvida pelo resistor. Primeiro, vamos calcular a tensão no resistor:
Então a potência média absorvida no resistor será:
Ué! A potência fornecida pela fonte é a mesma potência que o resistor absorve?
Sim! Apenas cargas resistivas absorvem potência, capacitores e indutores não absorvem potência. Nunca esqueça disso!
Também podemos encontrar a potência absorvida pelo resistor através da fórmula:
Onde .
Esse é o conjugado da corrente , ou seja se , então . Ou na forma polar: então .
Máxima transferência de potência média
Quando falamos em máxima transferência de potência temos que ter em mente o teorema de Thévenin. No circuito abaixo termos o circuito equivalente de Thévenin conectado a uma carga .
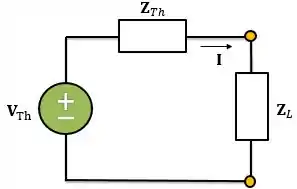
Sendo e .
A máxima transferência de potência média ocorre quando a impedância da carga é igual ao conjugado complexo da impedância de Thévenin, ou seja:
Quando isso ocorre, a máxima potência média é
Vamos fazer um exemplo. No circuito abaixo, vamos calcular o valor de que maximiza a potência média absorvida do circuito e qual o valor dessa potência.
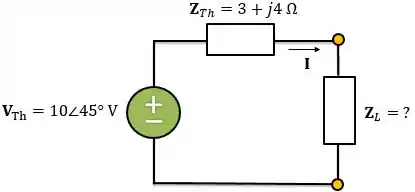
Como temos:
A gente tem que só mudar o sinal da parte imaginária e pronto.
Já a potência será:
Pronto!
Valor eficaz ou RMS
O valor eficaz de uma função periódica é a raiz quadrada da média do quadrado do sinal periódico. Confuso, né? Vamos com calma.
Para qualquer função periódica , o valor eficaz é:
Ele também é conhecido como raiz do valor médio quadrático (root-mean-square), ou simplesmente de valor RMS.
Por exemplo, vamos calcular o valor eficaz ou RMS para a senoide .
Como a média de uma senoide ao longo de seu período é zero, temos:
Então, quando a função é senoidal, para encontrarmos o valor RMS basta dividirmos a amplitude por .
O valor RMS de uma corrente periódica corresponde a uma corrente CC que fornece a mesma potência média para um resistor que a corrente periódica.
Ou seja, tanto aplicando uma fonte de corrente CA periódica quanto aplicando uma fonte de corrente CC que possui o valor eficaz da fonte CA, o resistor absorverá a mesma potência.
Portanto, podemos encontrar a potência média absorvida em um resistor com essas equações abaixo:
Agora vamos praticar!
Potência média
Máxima transferência de potência média
Valor eficaz ou RMS
Exercícios Resolvidos
Exercício Resolvido #1
Livro Sadiku, p.435, Problema 11.1
Se e , calcule a potência instantânea e a potência média.
Passo 1
Como vimos na teoria, a potência instantânea é a potência em qualquer instante e nada mais é do que o produto da tensão instantânea e a corrente instantânea .
Passo 2
Como a corrente está escrita em termos de seno, precisamos passá-la para cosseno:
Então, como e , vamos calcular a potência instantânea.
Lembrando da identidade trigonométrica
Temos:
Passo 3
Para encontrarmos a potência média é só aplicar a formula abaixo:
Substituindo os valores:
Resposta
Exercício Resolvido #2
Livro Sadiku, p.435, Problema 11.2
Dado o circuito abaixo, determine a potência média fornecida ou absorvida por elemento.
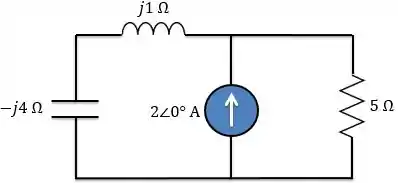
Passo 1
Como vimos na teoria, apenas cargas resistivas absorvem potência. Capacitores e indutores não absorvem potência. Então, a potência absorvida no resistor será igual a potência fornecida pela fonte.
Passo 2
Vamos calcular a potência absorvida pelo resistor através da formula:
Para isso, precisamos encontrar a corrente que passa pelo resistor. Então, aplicando divisor de corrente no circuito abaixo, temos:
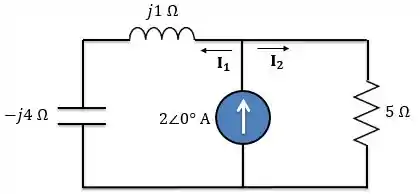
Passando para forma polar:
Passo 3
Aplicando a fórmula:
Portanto, a potência absorvida pelo resistor e fornecida pela fonte de corrente é . Além disso, o indutor e o capacitor não absorvem potência.
Resposta
A potência absorvida pelo resistor e fornecida pela fonte de corrente é . Além disso, o indutor e o capacitor não absorvem potência.
Exercício Resolvido #3
Livro Sadiku, p.435, Problema 11.8
No circuito abaixo, determine a potência média absorvida pelo resistor de .
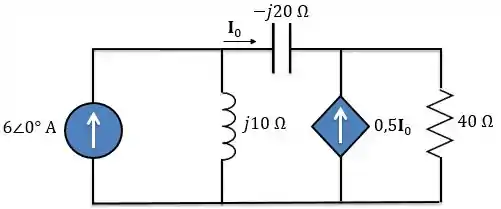
Passo 1
Como vimos na teoria, apenas cargas resistivas absorvem potência. Capacitores e indutores não absorvem potência. Vamos calcular a potência absorvida pelo resistor através da formula:
Passo 2
Precisamos encontrar a corrente que passa pelo resistor. Para isso, vamos fazer uma análise nodal no circuito.
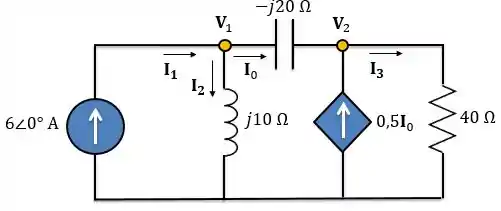
Aplicando a LCK ao nó 1:
Substituindo:
Aplicando a LCK ao nó 2:
Substituindo:
Passo 3
Isolando na primeira equação:
Agora substituindo na segunda:
Passo 4
Pela lei de Ohm, temos no resistor de :
Agora que temos a corrente que passa pelo resistor de . Podemos encontrar a potência media absorvida por esse resistor através da fórmula:
Resposta
Exercício Resolvido #4
Livro Sadiku, p.437, Problema 11.27
Calcule o valor RMS da forma de onda de corrente abaixo:
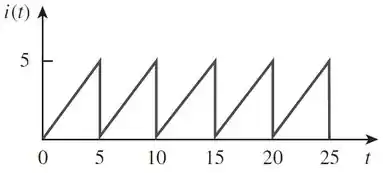
Passo 1
Primeiro temos que encontrar a expressão de . Analisando a onda vemos que seu período é . Logo:
Além disso, nesse período a forma de onda da corrente é uma reta:
Passo 2
Agora, é só jogar na fórmula e calcular o valor RMS:
Resposta
Exercício Resolvido #5
Livro Sadiku, p.437, Problema 11.22
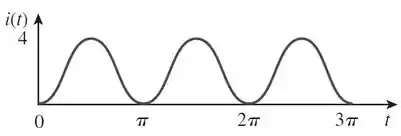
Determine o valor RMS da onda senoidal deslocada abaixo:
Passo 1
Primeiro temos que encontrar a expressão de . Analisando a onda vemos que seu período é . Logo:
Como
Temos:
Além disso, o seu valor de um pico ao outro é . Portanto a sua amplitude será:
Então, já sabemos que parte da expressão terá o termo abaixo:
Passo 2
Agora, vamos analisar o deslocamento. Para isso, vamos escolher um ponto do gráfico. Por exemplo a origem . Substituindo na expressão que temos até agora:
No gráfico, quando a corrente vale zero. Logo, para nossa expressão está de acordo com a onda do gráfico precisamos que o seu valor na origem seja zero. Temos duas formas de fazer isso:
Para verificarmos qual é a que corresponde ao gráfico, vamos escolher um novo ponto. Por exemplo, quando .
Substituindo em
Esse resultado não está de acordo com o gráfico, já que em a corrente vale .
Substituindo em
Esse resultado bate com o gráfico! Logo a expressão que descreve o gráfico é:
Passo 3
Agora, vamos calcular o valor RMS:
Lembrando que a integral ao longo do período de uma função senoidal é zero
e da relação
temos:
Resposta
Exercício Resolvido #6
Livro Sadiku, p.437, Problema 11.27
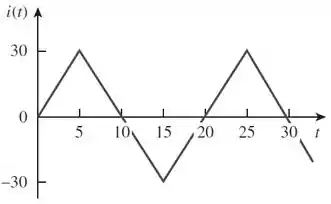
Calcule o valor eficaz da forma de onda de corrente abaixo e a potência média liberada para um resistor de , quando a corrente percorre o resistor.
Passo 1
Primeiro temos que encontrar a expressão de . Analisando a onda vemos que seu período é . Logo:
Para facilitar a nossa análise, vamos encontrar a expressão para corrente no intervalo .
No intervalo a forma de onda da corrente é uma reta decrescente. Sabemos que a equação de uma reta qualquer é:
No nosso caso, e , logo:
Vamos encontrar e , escolhendo dois pontos nesse intervalo. O primeiro ponto será:
Substituindo na equação da reta:
Fazendo a mesma coisa para , temos
Passo 2
Fazendo a equação menos a , temos:
Substituindo o valor de na equação :
Então, a expressão para corrente no intervalo é:
Passo 3
Agora, vamos fazer a mesma coisa para encontrar a expressão da corrente para o intervalo .
O primeiro ponto é . Substituindo na equação da reta:
Agora para :
Fazendo a equação menos a , temos:
Substituindo o valor de na equação :
Então, a expressão para corrente no intervalo é:
Passo 4
Agora que temos a expressão da corrente para todo o período é só jogar na fórmula e calcular o valor RMS:
Passo 5
Agora, precisamos encontrar a potência média liberada no resistor de quando essa corrente percorre o resistor. Para isso, basta aplicar a formula abaixo:
Moleza, né?!
Resposta
Exercício Resolvido #7
Livro Sadiku, p.436, Problema 11.13
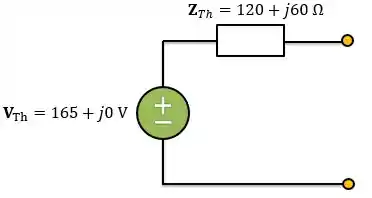
A impedância de Thevenin de uma fonte é , enquanto a tensão de Thevenin de pico é . Determine a potência média máxima disponível da fonte.
Passo 1
Vamos montar o circuito equivalente de Thevenin que o enunciado descreve:
Passo 2
Agora é só lembrar que e da fórmula:
Sendo,
Ou seja, é só pegar o módulo do fasor e elevar ao quadrado.
Substituindo os valores:
Resposta
Exercício Resolvido #8
Livro Sadiku, p.436, Problema 11.12
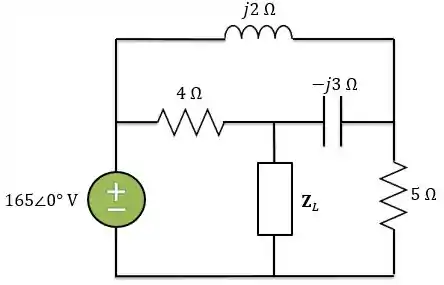
Para o circuito abaixo, determine a impedância da carga para a transferência de potência máxima (para ). Calcule a potência máxima absorvida pela carga.
Passo 1
Quando falamos em máxima transferência de potência temos que ter em mente o teorema de Thévenin. Para começar, precisamos encontrar o circuito equivalente de Thevenin conectado a carga . Para analisarmos um circuito como o abaixo:
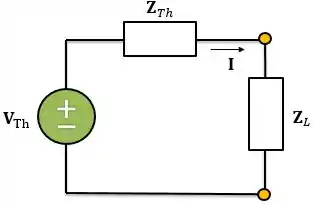
Passo 2
Para encontrar a impedância de Thevenin, desligamos a fonte de tensão, retiramos a carga e calculamos a impedância equivalente vista por seus terminais. Sempre lembrando que desligar uma fonte de tensão é o mesmo que substituí-la por um curto-circuito.
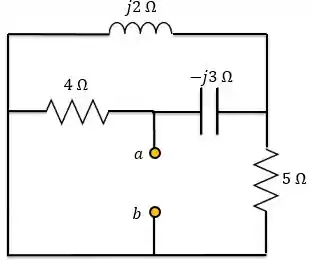
Vamos redesenhar o circuito para facilitar:
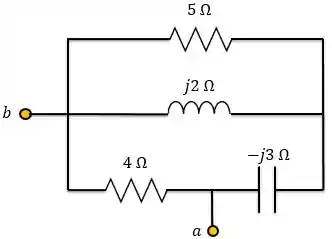
Primeiro, vamos calcular a impedância equivalente correspondente ao paralelo do resistor de com o indutor:
Então, agora temos o seguinte circuito:
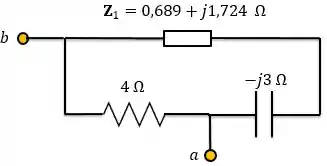
Como podemos ver, a impedância está em série com o capacitor. Portanto:
E o circuito fica assim:
Agora temos que calcular paralelo de e o resistor, que será a impedância de Thevenin.
Passando para forma retangular:
Passo 3
Como vimos na teoria, a máxima transferência de potência ocorre quando a impedância da carga é o conjugado da impedância de Thevenin, ou seja:
Então, lembrando que para obter o conjugado temos que inverter o sinal na parte imaginária, a impedância da carga será:
Passo 4
Agora falta calcularmos a potência máxima transferida, que tem a seguinte fórmula:
Para a gente poder usá-la precisamos encontrar o valor da tensão de Thevenin. Vamos fazer isso agora. Lembrando que é a tensão de circuito aberto nos terminais , vamos analisar o circuito abaixo:
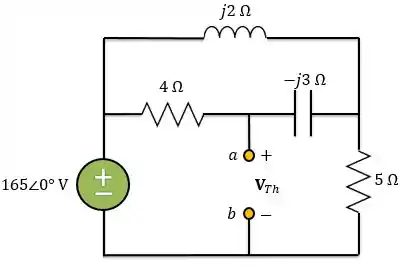
Vamos preparar o circuito para usar análise nodal:
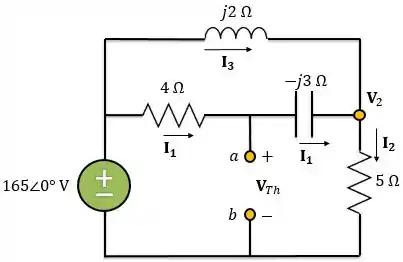
Aplicando a lei das correntes de Kirchhoff ao nó da tensão nodal :
Escrevendo em função das tensões nodais:
Passo 5
Agora que encontramos o valor de , podemos substituí-lo na equação abaixo para encontrarmos :
Estamos quase lá! Para finalmente encontrarmos , vamos aplicar a lei das tensões de Kirchhoff na malha abaixo:
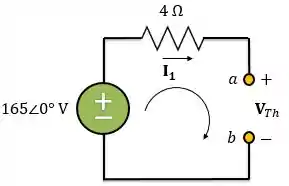
Passo 6
Agora é só lembrar que e da fórmula:
Sendo,
Ou seja, é só pegar o módulo do fasor e elevar ao quadrado.
Como,
Substituindo os valores:
Resposta
Exercício Resolvido #9
Livro Sadiku, Problema 11.3
Uma carga é formada por um resistor de em paralelo com um capacitor de . Se a carga for conectada a uma fonte de tensão , determine a potência média liberada para a carga.
Passo 1
Vamos começar desenhando o circuito pra ficar mais fácil de entender
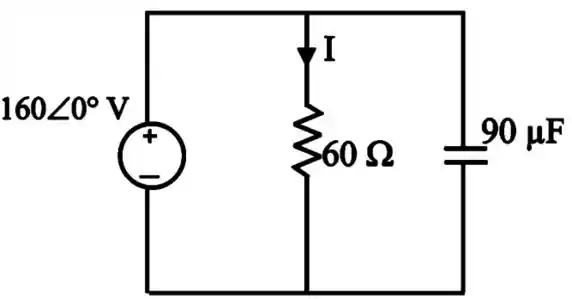
Passo 2
Agora vamos calcular a corrente usando a Primeira Lei de Ohm
A corrente é:
Passo 3
Agora pra calcular a potência média liberada, é só usar a fórmula:
Resposta
Exercício Resolvido #10
Livro Sadiku, Problema 11.6
Para o circuito da figura, .Determine a potência média absorvida pelo resistor de.
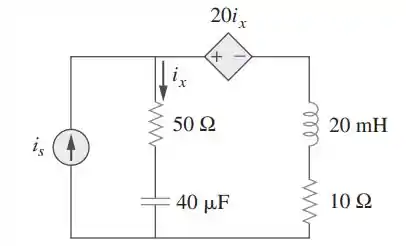
Passo 1
Vamos primeiro converter as grandezas para o domínio da frequência, ou seja,
Em seguida, calculamos as impedâncias no domínio da frequência também, sabendo que :
Para o indutor:
(lembrando que tudo tem que estar no Sistema Internacional)
Para o capacitor:
Passo 2
Agora vamos redesenhar o circuito com os valores encontrados no passo 1
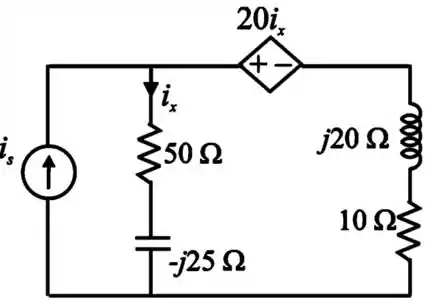
Passo 3
Vamos então aplicar a Lei das Correntes de Kirchhoff ao único nó do circuito (vamos chamar sua tensão de para encontrar o a partir da Lei de Ohm, veja:
Mas… quem é ?
Pela Lei de Ohm, , então, substituindo isso na equação anterior…
E agora sim podemos calcular o apenas substituindo esse valor:
Seu valor será
Passo 4
Então, a potência média absorvida pelo resistor de será: