Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Análise de Circuitos Trifásicos Desequilibrados

Ver Todos os Exercícios

Teoria

E aí, beleza?

Nesse tópico vamos analisar os circuitos trifásicos   Y - Y desequilibrados a 4 fios. Para ver onde o neutro da carga e da fonte podem estar sendo conectados e como fazemos para resolver esses tipos de circuito.

Neutro N (da carga) isolado

Nesse circuito o neutro da fonte trifásica ( n ) está ligado ao terra e o neutro da carga ( N ) está isolado, ou seja, não está ligado ao terra.

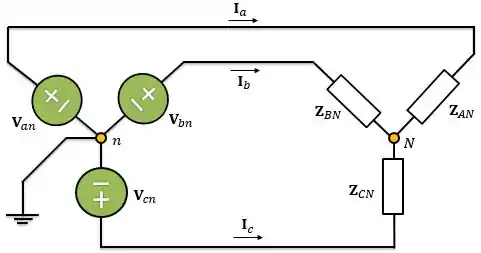
Para circuitos desse tipo nós utilizamos a análise nodal. Vamos fazer um exemplo numérico para ver como funciona. Vamos calcular as correntes de linha supondo que

V a n = 20 ∠ 0 °   V

V b n = 40 ∠ - 30 °   V

V c n = 60 ∠ 30 °   V

e que a carga trifásica é equilibrada com

Z A N = Z B N = Z C N = 20   Ω Passo 1:

Temos que considerar que existe uma tensão entre o neutro da carga ( N ) e a terra que vamos nomeá-la de V N .

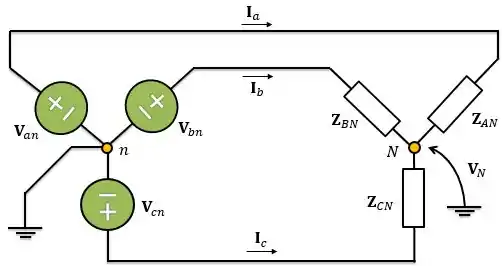
Além disso, aplicando a lei das correntes de Kirchhoff em um dos nós:

I a + I b + I c = 0

Passo 2:

Para facilitar a nossa análise, vamos redesenhar o circuito e fazer o esquema abaixo:

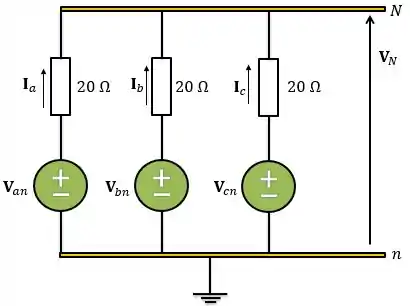
Agora vamos escrever as correntes em função das tensões:

I a = V a n - V N 20

I b = V b n - V N 20

I c = V c n - V N 20

Passo 3:

Substituindo na equação nodal, temos:

I a + I b + I c = 0

V a n - V N 20 + V b n - V N 20 + V c n - V N 20 = 0

V a n + V b n + V c n - 3 V N 20 = 0

V a n + V b n + V c n - 3 V N = 0

V N = 1 3 V a n + V b n + V c n

Como,

V a n = 20 ∠ 0 °   V

V b n = 40 ∠ - 30 °   V

V c n = 6 0 ∠ 30 °   V

Substituindo temos:

V N = 1 3 20 ∠ 0 ° + 40 ∠ - 30 ° + 60 ∠ 30 °

V N = 1 3 107,07 ∠ 5,36 °

V N = 35,7 ∠ 5,36 °   V

Passo 4:

Agora que calculamos a tensão V N , vamos substituir para encontrar as correntes:

I a = V a n - V N 20

I a = 20 ∠ 0 ° - 35,7 ∠ 5,36 ° 20

I a = 0,794 ∠ - 167,89 °   A

I b = V b n - V N 20

I b = 40 ∠ - 30 ° - 35,7 ∠ 5,36 ° 20

I b = 1,167 ∠ - 92,21 °   A

I c = V c n - V N 20

I c = 60 ∠ 30 ° - 35,7 ∠ 5,36 ° 20

I c = 1,566 ∠ 58,38 °   A

Vamos conferir se a soma das correntes deu zero mesmo:

0,794 ∠ - 167,89 ° + 1,167 ∠ - 92,21 ° + 1,566 ∠ 58,38 °

- 0,776 - j 0,166 + - 0,045 - j 1,167 + 0,821 + j 1,333

- 0,776 - 0,045 + 0,821 + j - 0,166 - 1,167 + 1,333

0 + j 0 = 0

Show de bola! Deu certo!

Então, seguindo esses passos não tem erro:

  1. Considerar que existe uma tensão entre o neutro da carga e a terra V N e aplicar a LCK em um dos nós;
  2. Redesenhar o circuito e escrever as correntes em função das tensões;
  3. Calcular V N ;
  4. Substituir o valor encontrado de V N nas equações de cada corrente e calculá-las.

Neutro N (da carga) solidamente aterrado

Nesse circuito o neutro da fonte trifásica ( n ) está ligado ao terra e o neutro da carga ( N ) também está ligado ao terra, ou seja, os dois neutros estão ligados ao terra.

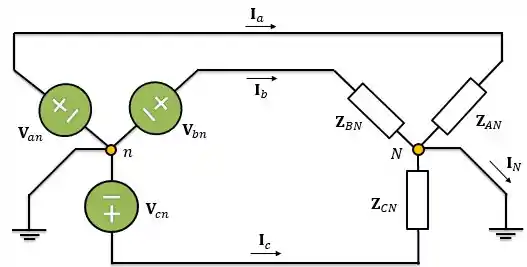
Esse é caso é mais simples. Porque como o neutro da carga está ligado à terra, seu potencial é zero e podemos desconsiderá-lo em nossa análise nodal.

V N = 0   V

Logo, como os dois neutros estão ligados à terra podemos conectá-los e nossa análise é mais simples:

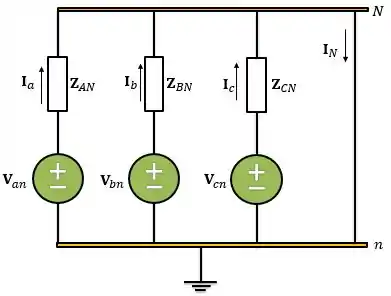
Aplicando a LCK ao nó da carga, temos:

I N = I a + I b + I c

Onde:

I a = V a n Z A N

I b = V b n Z B N

I c = V c n Z C N

Logo, utilizando os dados do exemplo anterior:

V a n = 20 ∠ 0 °   V

V b n = 40 ∠ - 30 °   V

V c n = 60 ∠ 30 °   V

Z A N = Z B N = Z C N = 20   Ω

As correntes serão de linha serão:

I a = 20 ∠ 0 ° 20 = 1 ∠ 0 °   A

I b = 40 ∠ - 30 ° 20 = 2 ∠ - 30 °   A

I c = 60 ∠ 30 ° 20 = 3 ∠ 30 °   A

E a corrente de neutro:

I N = 1 ∠ 0 ° + 2 ∠ - 30 ° + 3 ∠ 30 °

I N = 1 + 1,73 - j + 2,6 + j 1,5

I N = 5,33 + j 0,5   A

I N = 5,35 ∠ 5,36 °   A

Neutro N (da carga) aterrado por um resistor

Esse circuito é bem parecido com o circuito anterior, mas nesse o neutro da carga não está diretamente ligado à terra. Ele está ligado a um resistor que está conectado à terra. Se liga como é no circuito abaixo:

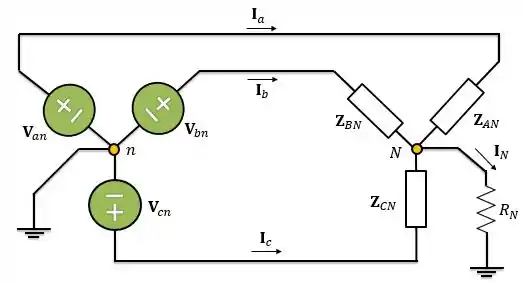
Logo, é como se existisse uma resistência entre o neutro da fonte ( n ) e o neutro da carga ( N ) . Além disso, devido à presença desse resistor, temos que considerar a tensão V N entre o neutro da carga ( N ) e a terra.

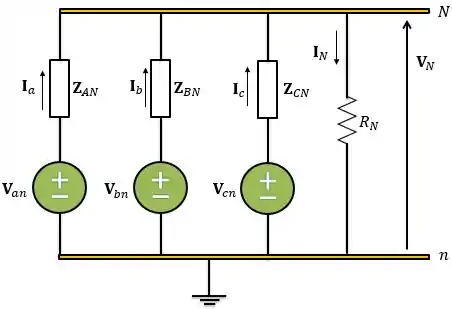
Então, utilizando os mesmos dados dos exemplos anteriores:

V a n = 20 ∠ 0 °   V

V b n = 40 ∠ - 30 °   V

V c n = 60 ∠ 30 °   V

Z A N = Z B N = Z C N = 20   Ω

E considerando que a resistência do neutro R N é 10   Ω , vamos encontrar a corrente que circula pelo neutro.

Passo 1:

Aplicando a LCK ao nó da carga, temos:

I N = I a + I b + I c

Agora vamos escrever as correntes em função das tensões:

I a = V a n - V N 20

I b = V b n - V N 20

I c = V c n - V N 20

I N = V N 10

Passo 2:

Agora, vamos substituir na equação nodal para determinarmos a tensão V N :

V N 10 = V a n - V N 20 + V b n - V N 20 + V c n - V N 20

2 V N 20 = V a n - V N 20 + V b n - V N 20 + V c n - V N 20

2 V N = V a n - V N + V b n - V N + V c n - V N

5 V N = V a n + V b n + V c n

V N = 1 5 ( V a n + V b n + V c n )

V N = 1 5 20 ∠ 0 ° + 40 ∠ - 30 ° + 60 ∠ 30 °

V N = 1 5 107,07 ∠ 5,36 °

V N = 21,41 ∠ 5,36 °   V

Passo 3:

Portanto, a corrente que que circula pelo neutro será:

I N = V N 10

I N = 21,41 ∠ 5,36 ° 10

I N = 2,14 ∠ 5,36 °   A

Pronto! Sabendo disso você vai detonar os exercícios! Pratica lá!

Neutro N (da carga) solidamente aterrado

Neutro N (da carga) aterrado por um resistor

Exercícios Resolvidos

Exercício Resolvido #1

UFRJ - Departamento de Engenharia Elétrica - Material Professor Heloi - 1

Considere o sistema estrela-estrela com neutro da carga isolado mostrado na figura abaixo.

Adotando

V a n = 10 ∠ 0 °   V

V b n = 20 ∠ - 60 °   V

V c n = 20 ∠ 60 °   V

e que a carga trifásica é equilibrada com

R = 10   Ω

Determine as correntes de linha I a , I b e I c .

Passo 1

Temos que considerar que existe uma tensão entre o neutro da carga ( N ) e a terra que vamos nomeá-la de V N .

Além disso, aplicando a lei das correntes de Kirchhoff em um dos nós:

I a + I b + I c = 0

Passo 2

Para facilitar a nossa análise, vamos redesenhar o circuito e fazer o esquema abaixo:

Agora vamos escrever as correntes em função das tensões:

I a = V a n - V N 10

I b = V b n - V N 10

I c = V c n - V N 10

Passo 3

Substituindo na equação nodal, temos:

I a + I b + I c = 0

V a n - V N 10 + V b n - V N 10 + V c n - V N 10 = 0

V a n + V b n + V c n - 3 V N 10 = 0

V a n + V b n + V c n - 3 V N = 0

V N = 1 3 V a n + V b n + V c n

Como,

V a n = 10 ∠ 0 °   V

V b n = 20 ∠ - 60 °   V

V c n = 20 ∠ 60 °   V

Substituindo temos:

V N = 1 3 10 ∠ 0 ° + 20 ∠ - 60 ° + 20 ∠ 60 °

V N = 1 3 10 + 10 - j 17,32 + 10 + j 17,32

V N = 1 3 ( 30 )

V N = 10 ∠ 0 °   V

Passo 4

Agora que calculamos a tensão V N , vamos substituir para encontrar as correntes:

I a = V a n - V N 1 0

I a = 10 ∠ 0 ° - 10 ∠ 0 °   1 0

I a = 0   A

I b = V b n - V N 1 0

I b = 20 ∠ - 60 °   - 10 ∠ 0 °   1 0

I b = 10 - j 17,32 - 10 10

I b = - j 17,32 10

I b = - j 1,732   A

I b = 1,732 ∠ - 90 °   A

I c = V c n - V N 20

I c = 20 ∠ 60 °   - 10 ∠ 0 ° 1 0

I c = 10 + j 17,32 - 10 10

I c = j 1,732   A

I c = 1,732 ∠ 90 °   A

Resposta

I a = 0   A

I b = 1,732 ∠ - 90 °   A

I c = 1,732 ∠ 90 °   A

Exercício Resolvido #2

UFRJ - Departamento de Engenharia Elétrica - Material Professor Heloi - 2

Considere o sistema estrela-estrela com neutro da carga solidamente aterrado mostrado na figura abaixo.

Adotando

V a n = 10 ∠ 0 °   V

V b n = 20 ∠ - 60 °   V

V c n = 20 ∠ 60 °   V

e que a carga trifásica é equilibrada com

R = 10   Ω

Determine as correntes de linha I a , I b , I c e   I n .

Passo 1

Como o neutro da carga está ligado à terra, seu potencial é zero e podemos desconsiderá-lo em nossa análise nodal.

V N = 0   V

Passo 2

Então, como os dois neutros estão ligados à terra podemos conectá-los e nossa análise fica assim:

Aplicando a LCK ao nó da carga, temos:

I N = I a + I b + I c

Onde:

I a = V a n Z A N

I b = V b n Z B N

I c = V c n Z C N

Passo 3

Logo, utilizando os dados do enunciado:

V a n = 1 0 ∠ 0 °   V

V b n = 20 ∠ - 6 0 °   V

V c n = 20 ∠ 6 0 °   V

R = 1 0   Ω

As correntes serão de linha serão:

I a = 1 0 ∠ 0 ° 1 0 = 1 ∠ 0 °   A

I b = 20 ∠ - 6 0 ° 1 0 = 2 ∠ - 6 0 °   A

I c = 20 ∠ 6 0 ° 1 0 = 2 ∠ 6 0 °   A

Passo 4

Agora que temos as correntes de linha, vamos soma-las para encontrarmos a corrente que circula no neutro:

I N = 1 ∠ 0 ° + 2 ∠ - 60 ° + 2 ∠ 6 0 °

I N = 1 + 1 - j 1,73 2 + 1 + j 1,732

I N = 3   A

I N = 3 ∠ 0 °   A

Resposta

I a = 1 ∠ 0 °   A

I b = 2 ∠ - 60 °   A

I c = 2 ∠ 60 °   A

I N = 3 ∠ 0 °   A

Exercício Resolvido #3

UFRJ - Departamento de Engenharia Elétrica - Material Professor Heloi - 3

Considere o sistema estrela-estrela com neutro da carga aterrado por meio de um resistor de 5   Ω mostrado na figura abaixo:

Adotando

V a n = 10 ∠ 0 °   V

V b n = 20 ∠ - 60 °   V

V c n = 20 ∠ 60 °   V

e que a carga trifásica é equilibrada com

R = 10   Ω

Determine as correntes de linha I a , I b , I c e   I n .

Passo 1

Nesse circuito o neutro da carga não está diretamente ligado à terra. Ele está ligado a um resistor que está conectado à terra.

Passo 2

Logo, é como se existisse uma resistência entre o neutro da fonte ( n ) e o neutro da carga ( N ) . Além disso, devido à presença desse resistor, temos que considerar a tensão V N entre o neutro da carga ( N ) e a terra.

Passo 3

Então, utilizando os mesmos dados do enunciado:

V a n = 1 0 ∠ 0 °   V

V b n = 20 ∠ - 6 0 °   V

V c n = 20 ∠ 6 0 °   V

R = 1 0   Ω

E considerando que a resistência do neutro R N é 5   Ω , vamos encontrar a corrente que circula pelo neutro.

Aplicando a LCK ao nó da carga, temos:

I N = I a + I b + I c

Passo 4

Agora vamos escrever as correntes em função das tensões:

I a = V a n - V N 1 0

I b = V b n - V N 1 0

I c = V c n - V N 1 0

I N = V N 5

Substituindo na equação nodal para determinarmos a tensão V N :

V N 5 = V a n - V N 1 0 + V b n - V N 1 0 + V c n - V N 1 0

2 V N 1 0 = V a n - V N 1 0 + V b n - V N 1 0 + V c n - V N 1 0

2 V N = V a n - V N + V b n - V N + V c n - V N

5 V N = V a n + V b n + V c n

V N = 1 5 ( V a n + V b n + V c n )

V N = 1 5 10 ∠ 0 ° + 20 ∠ - 60 ° + 20 ∠ 6 0 °

V N = 1 5 10 + 10 - j 17,32 + 10 + j 17,32

V N = 1 5 ( 30 )

V N = 6 ∠ 0 °   V

Passo 5

Portanto, a corrente que circula pelo neutro será:

I N = V N 5

I N = 6 ∠ 0 ° 5

I N = 1,2 ∠ 0 °   A

Passo 6

Falta calcularmos as correntes de linha. Substituindo pelos valores que encontramos, temos:

I a = V a n - V N 10

I a = 10 ∠ 0 ° - 6 ∠ 0 ° 10

I a = 4 ∠ 0 ° 10

I a = 0 , 4 ∠ 0 °   A

I b = V b n - V N 10

I b = 20 ∠ - 60 °   - 6 ∠ 0 ° 10

I b = 10 - j 17,32 - 6 10

I b = 4 - j 17,32 10

I b = 17,77 ∠ - 76,99 ° 10

I b = 1,78 ∠ - 76,99 °   A

I c = V c n - V N 10

I c = 20 ∠ 60 °   - 6 ∠ 0 ° 10

I c = 10 + j 17,32 - 6 10

I c = 4 + j 17,32 10

I c = 17,77 ∠ 76,99 ° 10

I c = 1,78 ∠ 76,99 °   A

Resposta

I a = 0,4 ∠ 0 °   A

I b = 1,78 ∠ - 76,99 °   A

I c = 1,78 ∠ 76,99 °   A

I N = 1,2 ∠ 0 °   A

Exercício Resolvido #4

UDESC – Eletrotécnica (adaptado)

Encontre I 0 no circuito abaixo, considerando que a fonte trifásica é equilibrada com sequência de fase a b c .

Passo 1

Nesse circuito, além das cargas trifásicas, temos uma impedância em cada linha Z l = 0,8 + j 4   Ω . Além disso, o neutro da carga está ligado ao neutro da fonte através de uma impedância de 20   Ω e como a sequência da fonte trifásica equilibrada é a b c , temos:

V a n = 480 ∠ 0 °   V

V b n = 480 ∠ - 120 °   V

V c n = 480 ∠ 120 °   V

Passo 2

Devido à presença desse resistor, temos que considerar a tensão V 0 entre o neutro da carga e o neutro da fonte. Então, temos a seguinte análise nodal:

Onde:

Z l + Z A N = 1 + j 5,6 + ( 79 + j 54,4 )

Z l + Z A N = 80 + j 60   Ω

Z l + Z A N = 100 ∠ 36,87 °   Ω

Z l + Z B N = 1 + j 5,6 + ( 39 + j 24,4 )

Z l + Z B N = 40 + j 30   Ω

Z l + Z B N = 50 ∠ 36,87 °   Ω

Z l + Z C N = 1 + j 5,6 + ( 159 + j 11 4,4 )

Z l + Z C N = 16 0 + j 12 0   Ω

Z l + Z C N = 2 00 ∠ 36,87 °   Ω

Passo 3

Aplicando a LCK ao nó da carga, temos:

I 0 = I a + I b + I c

Agora vamos escrever as correntes em função das tensões:

I a = V a n - V 0 Z l + Z A N

I b = V b n - V N Z l + Z B N

I c = V c n - V N Z l + Z C N

I 0 = V 0 20

Substituindo na equação nodal para determinarmos a tensão V N :

V 0 20 = V a n - V 0 Z l + Z A N + V b n - V N Z l + Z B N + V c n - V N Z l + Z C N

V 0 2 0 = 480 ∠ 0 ° - V 0 100 ∠ 36,87 ° + 480 ∠ - 120 ° - V 0 50 ∠ 36,87 ° + 480 ∠ 120 ° - V 0 200 ∠ 36,87 °

0,05 V 0 = 4,8 ∠ - 36,87 ° - 0,01 ∠ - 36,87 ° V 0 + 9,6 ∠ - 15 6,87 ° - ( 0,02 ∠ - 36,87 ° ) V 0 + 2,4 ∠ 83,13 ° - ( 0,005 ∠ - 36,87 ° ) V 0

0,05 V 0 = 4 , 8 ∠ - 36,87 ° + 9,6 ∠ - 15 6,87 ° + 2,4 ∠ 83,13 ° - ( 0,035 ∠ - 36,87 ° ) V 0

0,05 V 0 + ( 0,035 ∠ - 36,87 ° ) V 0 = 3,84 - j 2,88 - 8,83 - j 3,77 + 0,287 + j 2,38

( 0,05 + 0,028 - j 0,021 ) V 0 = - 4,7 - j 4,27

( 0 , 078 - j 0,021 ) V 0 = 6,35 ∠ - 137,75 °

V 0 = 6,35 ∠ - 137,75 ° 0,078 - j 0,021

V 0 = 6,35 ∠ - 137,75 ° ( 0,081 ∠ - 15,07 ° )

V 0 = 78,4 ∠ - 122,6 8 °   V

Passo 4

Portanto, pela lei de Ohm, a corrente que circula pelo neutro será:

I 0 = V 0 20

I 0 = 78,4 ∠ - 122,68 ° 20

I 0 = 3,92 ∠ - 122,68 °   A

Resposta

I 0 = 3,92 ∠ - 122,68 °   A

Exercício Resolvido #5

UNICAMP (adaptado)

Encontre as correntes de linha e a corrente que circula pelo neutro no circuito Y - 4 fios abaixo:

As impedâncias da carga por fase valem:

Z A = 100 = 100 ∠ 0 °   Ω

Z B = 30 - j 40 = 50 ∠ - 53,13 °   Ω

Z C = 50 + j 50 = 50 2 ∠ 45 °   Ω

Suponha que a fonte trifásica é equilibrada com sequência a b c e V a n = 100 ∠ 0 °   V .

Passo 1

Esse circuito nada mais é do que um circuito Y - Y a 4 fios com uma cara diferente. Vamos redesenhá-lo para a forma que conhecemos:

Como a sequência da fonte trifásica equilibrada é a b c , temos:

V a n = 100 ∠ 0 °   V

V b n = 100 ∠ - 120 °   V

V c n = 100 ∠ 120 °   V

Passo 2

Então, como os dois neutros estão interligados, nossa análise fica assim:

Aplicando a LCK ao nó da carga, temos:

I N = I a + I b + I c

Onde:

I a = V a n Z A

I b = V b n Z B

I c = V c n Z C

Passo 3

Logo, utilizando os dados do enunciado, as correntes de linha serão:

I a = 100 ∠ 0 ° 100 ∠ 0 ° = 1 ∠ 0 °   A

I b = 100 ∠ - 120 ° 50 ∠ - 53,13 ° = 2 ∠ - 66,87 °   A

I c = 100 ∠ 120 ° 50 2 ∠ 45 ° = 1,414 ∠ 75 °   A

Passo 4

Agora que temos as correntes de linha, vamos somá-las para encontrarmos a corrente que circula no neutro:

I N = 1 ∠ 0 ° + 2 ∠ - 66,87 ° + 1,414 ∠ 75 °

I N = 1 + ( 0,786 - j 1,839 ) + ( 0,366 + j 1,366 )

I N = 2,152 - j 0,473   A

I N = 2,2 ∠ - 12,39 °   A

Resposta

I a = 1 ∠ 0 °   A

I b = 2 ∠ - 66,87 °   A

I c = 1,414 ∠ 75 °   A

I N = 2,2 ∠ - 12,39 °   A

Exercício Resolvido #6

UNESP - Engenharia Elétrica - cap1 - circuitos-trifasicos - 1.3.2 (adaptado)

Encontre as correntes de linha para o sistema abaixo com fonte trifásica equilibrada e carga desequilibrada com:

Z A = 79 + j 56   Ω

Z B = 39 + j 26   Ω

Z C = 159 + j 116   Ω

As impedâncias de cada linha são iguais e valem Z l = 1 + j 4   Ω . Suponha que a sequência é a b c e V a n = 120 ∠ 0 °   V .

Passo 1

Esse circuito nada mais é do que um circuito Y - Y com o neutro da carga isolado. Temos que considerar a impedância da linha e também que existe uma tensão entre o neutro da carga ( N ) e a terra que vamos nomeá-la de V N .

Vamos redesenhá-lo para a forma que conhecemos:

Como a sequência da fonte trifásica equilibrada é a b c , temos:

V a n = 120 ∠ 0 °   V

V b n = 120 ∠ - 120 °   V

V c n = 120 ∠ 120 °   V

Passo 2

Vamos desenhar nosso esquema para análise nodal:

Onde:

Z l + Z A = 1 + j 4 + ( 79 + j 56 )

Z l + Z A = 80 + j 60   Ω

Z l + Z A = 100 ∠ 36,87 °   Ω

Z l + Z B = 1 + j 4 + ( 39 + j 26 )

Z l + Z B = 40 + j 30   Ω

Z l + Z B = 50 ∠ 36,87 °   Ω

Z l + Z C = 1 + j 4 + ( 159 + j 116 )

Z l + Z C = 160 + j 120   Ω

Z l + Z C = 200 ∠ 36,87 °   Ω

Passo 3

Aplicando a LCK ao nó da carga, temos:

I a + I b + I c = 0

Agora vamos escrever as correntes em função das tensões:

I a = V a n - V N Z l + Z A

I b = V b n - V N Z l + Z B

I c = V c n - V N Z l + Z C

I N = V N Z N

Substituindo na equação nodal para determinarmos a tensão V N , temos:

V a n - V N Z l + Z A + V b n - V N Z l + Z B + V c n - V N Z l + Z C = 0

120 ∠ 0 ° - V N 100 ∠ 36,87 ° + 120 ∠ - 120 ° - V N 50 ∠ 36,87 ° + 120 ∠ 120 ° - V N 200 ∠ 36,87 ° = 0

1,2 ∠ - 36,87 ° - 0,01 ∠ - 36,87 ° V N + 2,4 ∠ - 156,87 ° - 0,02 ∠ - 36,87 ° V N + 0,6 ∠ 83,13 ° - 0,005 ∠ - 36,87 ° V N = 0

1,2 ∠ - 36,87 ° + 2,4 ∠ - 156,87 ° + 0,6 ∠ 83,13 ° - 0,035 ∠ - 36,87 ° V N = 0

( 0,035 ∠ - 36,87 ° ) V N = 0,96 - j 0,72 - 2,21 - j 0,943 + 0,072 + j 0,596

( 0,028 - j 0,021 ) V N = - 1,18 - j 1,07

( 0,0 28 - j 0,021 ) V N = 1,59 ∠ - 137,76 °

V N = 1,59 ∠ - 137,76 ° 0,0 28 - j 0,021

V N = 1,59 ∠ - 137,76 ° 0,035 ∠ - 36,87 °

V N = 45,43 ∠ - 100,89 °   V

Passo 4

Agora que temos a tensão entre os neutros, vamos calcular as correntes de linha:

I a = V a n - V N Z l + Z A

I a = 120 ∠ 0 °   - 45,43 ∠ - 100,89 ° 100 ∠ 36,87 °

I a = 136,10 ∠ 19,13 ° 100 ∠ 36,87 °

I a = 1,36 ∠ - 17,74 °   A

I b = V b n - V N Z l + Z B

I b = 120 ∠ - 120 ° - 45,43 ∠ - 100,89 ° 50 ∠ 36,87 °

I b = 78,49 ∠ - 130,92 ° 50 ∠ 36,87 °

I b = 1,57 ∠ - 1 67,79 °   A

I c = V c n - V N Z l + Z C

I c = 120 ∠ 120 ° - 45,43 ∠ - 100,89 ° 200 ∠ 36,87 °

I c = 157,18 ∠ 109,09 ° 200 ∠ 36,87 °

I c = 0,786 ∠ 72,22 °   A

Resposta

I a = 1,36 ∠ - 17,74 °   A

I b = 1,57 ∠ - 167,79 °   A

I c = 0,786 ∠ 72,22 °   A

Exercício Resolvido #7

UNESP - Engenharia Elétrica - cap1 - circuitos-trifasicos - 1.3.1 (adaptado)

Encontre as tensões de fase na carga para o sistema abaixo com fonte trifásica equilibrada e carga desequilibrada com:

Z A = 79 + j 56   Ω

Z B = 39 + j 26   Ω

Z C = 159 + j 116   Ω

As impedâncias de cada linha são iguais e valem Z l = 1 + j 4   Ω e a impedância do neutro é Z N = 10   Ω . Suponha que a sequência é a b c e V a n = 120 ∠ 0 °   V .

Passo 1

Esse circuito nada mais é do que um circuito Y - Y com o neutro da carga aterrado por uma impedância. Temos que tomar cuidado porque temos que considerar a impedância da linha também. Vamos redesenhá-lo para a forma que conhecemos:

Como a sequência da fonte trifásica equilibrada é a b c , temos:

V a n = 120 ∠ 0 °   V

V b n = 120 ∠ - 120 °   V

V c n = 120 ∠ 120 °   V

Passo 2

Nesse circuito o neutro da carga não está diretamente ligado à terra. Ele está ligado a um resistor que está conectado à terra. Então, é como se existisse uma resistência entre o neutro da fonte ( n ) e o neutro da carga ( N ) .

Além disso, devido à presença desse resistor, temos que considerar a tensão V N entre o neutro da carga ( N ) e a terra.

Onde:

Z l + Z A = 1 + j 4 + ( 79 + j 56 )

Z l + Z A = 80 + j 60   Ω

Z l + Z A = 100 ∠ 36,87 °   Ω

Z l + Z B = 1 + j 4 + ( 39 + j 26 )

Z l + Z B = 40 + j 30   Ω

Z l + Z B = 50 ∠ 36,87 °   Ω

Z l + Z C = 1 + j 4 + ( 159 + j 116 )

Z l + Z C = 160 + j 120   Ω

Z l + Z C = 200 ∠ 36,87 °   Ω

Passo 3

Aplicando a LCK ao nó da carga, temos:

I N = I a + I b + I c

Agora vamos escrever as correntes em função das tensões:

I a = V a n - V N Z l + Z A

I b = V b n - V N Z l + Z B

I c = V c n - V N Z l + Z C

I N = V N Z N

Substituindo na equação nodal para determinarmos a tensão V N , temos:

V N Z N = V a n - V N Z l + Z A + V b n - V N Z l + Z B + V c n - V N Z l + Z C

V N 10 = 120 ∠ 0 ° - V N 100 ∠ 36,87 ° + 120 ∠ - 120 ° - V N 50 ∠ 36,87 ° + 120 ∠ 120 ° - V N 200 ∠ 36,87 °

0,1 V N = 1,2 ∠ - 36,87 ° - 0,01 ∠ - 36,87 ° V N + 2,4 ∠ - 156,87 ° - ( 0,02 ∠ - 36,87 ° ) V N + 0,6 ∠ 83,13 ° - ( 0,005 ∠ - 36,87 ° ) V N

0,1 V N = 1,2 ∠ - 36,87 ° + 2,4 ∠ - 156,87 ° + 0,6 ∠ 83,13 ° - ( 0,035 ∠ - 36,87 ° ) V N

0,1 V N + ( 0,035 ∠ - 36,87 ° ) V N = 0,96 - j 0,72 - 2,21 - j 0,943 + 0,072 + j 0,596

( 0,1 + 0,028 - j 0,021 ) V N = - 1,18 - j 1,07

( 0,128 - j 0,021 ) V N = 1,59 ∠ - 137,76 °

V N = 1,59 ∠ - 137,76 ° 0,128 - j 0,021

V N = 1,59 ∠ - 137,76 ° 0,130 ∠ - 9,32 °

V N = 12,23 ∠ - 128,44 °   V

Passo 4

Agora que temos a tensão entre os neutros, vamos calcular as correntes de linha:

I a = V a n - V N Z l + Z A

I a = 120 ∠ 0 °   - 12,23 ∠ - 128,44 ° 100 ∠ 36,87 °

I a = 127,96 ∠ 4,29 ° 100 ∠ 36,87 °

I a = 1,28 ∠ - 32,58 °   A

I b = V b n - V N Z l + Z B

I b = 120 ∠ - 120 ° - 12,23 ∠ - 128,44 ° 50 ∠ 36,87 °

I b = 107,92 ∠ - 119,05 ° 50 ∠ 36,87 °

I b = 2,16 ∠ - 155,92 °   A

I c = V c n - V N Z l + Z C

I c = 120 ∠ 120 ° - 12,23 ∠ - 128,44 ° 200 ∠ 36,87 °

I c = 125,01 ∠ 114,78 ° 200 ∠ 36,87 °

I c = 0,625 ∠ 77,91 °   A

Passo 5

Agora, finalmente podemos calcular as tensões de fase na carga. Para a fase A , temos:

V A N = I a Z A

V A N = ( 1,28 ∠ - 32,58 ° ) ( 79 + j 56 )

V A N = 1,28 ∠ - 32,58 ° 96,83 ∠ 35,33 °

V A N = 123,94 ∠ 2,75 °   V

Para fase B :

V B N = I b Z B

V B N = ( 2,16 ∠ - 155,92 °   ) ( 39 + j 26 )

V B N = 2,16 ∠ - 155,92 °   46,87 ∠ 33 , 69 °

V B N = 101,24 ∠ - 122,23 °   V

Para fase C :

V C N = I c Z C

V C N = ( 0,625 ∠ 77,91 ° ) ( 159 + j 116 )

V C N = ( 0,625 ∠ 77,91 ° ) ( 196,82 ∠ 36,11 ° )

V C N = 123,01 ∠ 114,02 °   V

Resposta

V A N = 123,94 ∠ 2,75 °   V

V B N = 101,24 ∠ 89,23 °   V

V C N = 123,01 ∠ 114,02 °   V

Exercício Resolvido #8

Livro Sadiku, Exemplo 12.9

A carga conectada em estrela desequilibrada da figura tem tensões equilibradas de 100 V e a sequência a c b . Calcule as correntes de linha e a corrente neutra. Adote Z A = 15 Ω ,   Z B = 10 + j 5 Ω e Z C = 6 - j 8 Ω .

Passo 1

Essa é bem simples!

Vamos utilizar a Primeira Lei de Ohm para corrente alternada, ou seja, trabalhando com fasores:

Para I a :

I a = 100 ∠ 0 ° 15 = 6.67 ∠ 0 °   A

Para I b :

I b = 100 ∠ 120 ° 10 + j 5

I b = 100 ∠ 120 ° 11.18 ∠ 26.56 ° = 8.94 ∠ 93.44 °   A

Para I c :

I c = 100 ∠ - 120 ° 6 - j 8 = 100 ∠ - 120 ° 10 ∠ - 53.13 ° = 10 ∠ - 66.87 °   A

Passo 2

Para achar a corrente de neutro:

I n =   - ( I a + I b + I c ) =   - ( 6.67 - 0.54 + j 8.92 + 3.93 - j 9.2 )

I n =   - 10.06 + j 0.28 = 10.06 ∠ 178.4 °   A

Resposta

I a = 6.67 ∠ 0 °   A

I b = 8.94 ∠ 93.44 °   A

I c = 10 ∠ - 66.87 °   A

I n = 10.06 ∠ 178.4 °   A

Exercício Resolvido #9

Livro Sadiku, Problema 12.86

Para o sistema monofásico trifilar na figura, determine as correntes I a A   , I b B e I n N .

Passo 1

Vamos analisar o circuito com suas correntes de Malha:

Passo 2

Vamos fazer a análise de malha da Malha 1:

- 240 ∠ 0 ° + 1 I 1 + ( 24 - j 2 ) I 1 + 1 ( I 1 - I 2 ) = 0

( 1 + 24 - j 2 + 1 ) I 1 - I 2 = 240

( 26 - j 2 ) I 1 - I 2 = 240

E também na Malha 2:

- 240 ∠ 0 ° + 1 ( I 2 - I 1 ) + ( 15 + j 4 ) I 2 + 1 I 2 = 0

- I 1 + ( 1 + 15 + j 4 + 1 ) I 2 = 240

- I 1 + ( 17 + j 4 ) I 2 = 240

Passo 3

Vamos resolver esse sistema de equações (da malha 1 e da malha 2) na forma matricial:

Agora, vamos achar primeiro o determinante dessa matriz e em seguida os determinantes das matrizes modificadas:

Passo 4

Para as correntes I 1 e I 2

I 1 = Δ 1 Δ = 4425.4 ∠ 12.53 ° 454.42 ∠ 8.86 ° = 9.74 ∠ 3.67 ° A

I 2 = Δ 2 Δ = 6497.8 ∠ - 4.24 ° 454.42 ∠ 8.86 ° = 14.3 ∠ - 13.1 °   A

Para as correntes de linha teremos:

I a = I 1 = 56.78   A

I c =   - I 2 = 42.75 ∠ - 155.1 °   A

I b = I 2 - I 1 = 38.78 + j 18 - 56.78 = 25.46 ∠ 135 °   A

Passo 5

Para a corrente I a A :

I a A = I 1

I a A = 97.4 ∠ 3.67 °   A

Para a corrente I b B :

I b B =   - I 2 =   - 14.4 ∠ 166.9 °   A

Para a corrente I n N :

I n N = I 2 - I 1

I n N = ( 14.3 ∠ - 13.1 ° ) - ( 9.74 ∠ 3.67 ° )

I n N = 5.71 ∠ - 42.56 °   A

Resposta

I a A = 97.4 ∠ 3.67 °   A

I b B =   - 14.4 ∠ 166.9 °   A

I n N = 5.71 ∠ - 42.56 °   A

Exercício Resolvido #10

Livro Sadiku, Problema 12.84

Para o circuito desequilibrado da figura, determine as correntes de linha

Passo 1

Vamos fazer a análise de malhas para encontrar as correntes necessárias.

Na malha 1:

120 ∠ - 120 ° - . 120 ∠ 0 ° + ( 10 + j 5 ) I 1 = 0

. ( 1 0 + j 5 ) I 1 - 10 I 2 = 120 3 . ∠ 30 °

Na malha 2:

120 ∠ 120 ° - . 120 ∠ - 120 ° + ( 10 - j 10 ) I 2 - 1 0 I 1 = 0

- 10 I 1 + ( 1 0 - j 10 ) I 2 = 120 3 . ∠ - 90 °

Passo 2

Vamos resolver esse sistema de equações (da malha 1 e da malha 2) na forma matricial:

Agora, vamos achar primeiro o determinante dessa matriz e em seguida os determinantes das matrizes modificadas:

Passo 3

Para as correntes I 1 e I 2

I 1 = Δ 1 Δ = 4015.23 ∠ ° 70.71 ∠ - 45 ° = 56.78 A

I 2 = Δ 2 Δ = 3023.4 ∠ - 20.1 ° 70.71 ∠ - 45 ° = 42.75 ∠ 24.9 °

Para as correntes de linha teremos:

I a = I 1 = 56.78   A

I c =   - I 2 = 42.75 ∠ - 155.1 °   A

I b = I 2 - I 1 = 38.78 + j 18 - 56.78 = 25.46 ∠ 135 °   A

Passo 4

I a = 56.78   A

I c = 42.75 ∠ - 155.1 °   A

I b = 25.46 ∠ 135 °   A

Resposta

Ei, a resposta está no passo a passo :)

Exercícios de Livros Relacionados

Use o PSpice ou MultiSim para determinar as correntes IaA e IaC no sistema trifásico desequilibrado mostrado na Figura 12.69. Seja Z l = 2 + j , Z 1 = 40 + j 20Ω Z 2 = 50 - j 30 Ω , Z 3 = 25Ω
Use o PSpice ou MultiSim para determinar Io no circuito monofásico trifilar da Figura 12.66. Seja Z 1 = 15-j 10Ω ,Z 2=30+j 20Ω eZ 3 = 12+j 5Ω .
Resolva o Problema 12.10 usando o PSpice ou MultiSim.
Considere a Figura 12.61 e elabore um problema que ajude outros estudantes a entender melhor sistemas trifásicos não equilibrados.
Um sistema trifásico quadrifilar operando com tensão de linha igual a 208V é mostrado na Figura 12.71. As tensões da fonte estão equilibradas. A potência absorvida pela carga resistiva conectada em es