Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 12.Problemas - Ex. 53

Considere a Figura 12.61 e elabore um problema que ajude outros estudantes a entender melhor sistemas trifásicos não equilibrados.

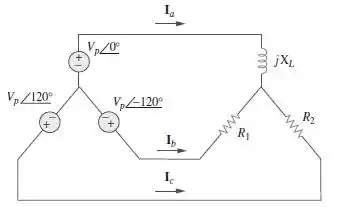
Passo 1

Este problema pode ser elaborado de inúmeros modos, mas vamos utilizar este exemplo.

No sistema estrela-estrela como mostra a figura abaixo, a carga é desequilibrada

  1. Calcule I a ,   I b , e I c
  2. Encontre a potência complexa total entregue a carga. Considere V p = 240   V   r m s

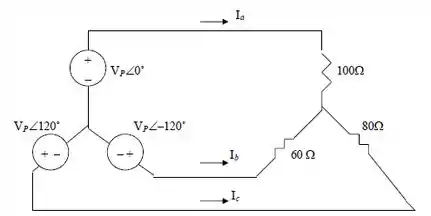
Passo 2

Podemos resolver por análise de malhas como mostra a figura abaixo,

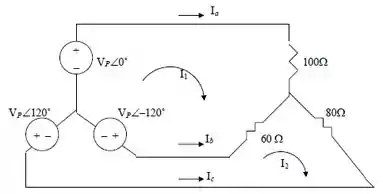
Portanto, teremos as seguintes equações

240 ∠ –120° – 240 + 160 I 1 – 60 I 2 = 0 ou 160 I 1 – 60 I 2 = 360+j207.84 (1)

240 ∠ 120° – 240 ∠ –120° – 60 I 1 + 140 I 2 = 0 ou – 60 I 1 + 140 I 2 = –j415.7 (2)

Assim a matriz para as equações (1) e (2) torna

160 - 60 - 60 140 I 1 I 2 = 360 + j 207.84 - j 415.7

Passo 3

Para resolver essas equações pode ser de várias maneiras, optou-se por usar o MATLAB, desse modo o código para a resolução é:

>> Z=[160,-60;-60,140]

Z =

160 -60

-60 140

>> V=[(360+207.8i);-415.7i]

V =

1.0e+002 *

3.6000 + 2.0780i

0 - 4.1570i

>> I=inv(Z)*V

I =

2.6809 + 0.2207i

1.1489 - 2.8747i

Assim, as correntes são

I 1 = 2.681 + j 0.2207

I 2 = 1.1489 - j 2.875

Note que,

I a = I 1 = 2.69 ∠ 4.71 °   A

I b = I 2 - I 1 = 3.454 ∠ - 116.33 °

I c =   - I 2 = 3.096 ∠ 111.78 °

Passo 4

Para a potência complexa podemos fazer de cada fase, e depois somar assim teremos a potência complexa total. Com isso

S a = I a 2 Z a = 2.69 2 * 100 = 723.61

S b = I b 2 Z b = 3.454 2 * 60 = 715.81

S c = I c 2 Z c = 3.0957 2 * 80 = 766.67

Portanto,

S = S a + S b + S c = 2.205   k V A

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um circuito estrela-estrela quadrifilar possui V a n = 120 ∠ 120 ° , V b n = 120 ∠ 0 ° V c n = 120 ∠ - 120 °V se as impedâncias forem Z A N = 20 ∠ 60 ° , Z B N = 30 ∠ 0 ° Z C N = 40 ∠ 30 °Ω Determine
Considere o sistema triângulo-triângulo mostrado na Figura 12.60. Adote Z 1 = 8 + j6 Ω , Z 2 = 4,2 – j2,2 Ω e Z 3 = 10 + j0 Ω .(a) Determine as correntes de fase I A B , I B C e I C A .(b) Calcule as
Uma fonte trifásica conectada em estrela equilibrada com V p = 210VR M S alimenta uma carga trifásica conectada em estrela com impedância por faseZ A=80Ω ,Z B=60+j 90ΩeZ C=j 80Ω . Calcule as correntes
Determine as correntes de linha para o circuito trifásico da Figura 12.64. Seja Va = 110 0 , Vb = 110l 120 e Vc = 110 120 V.
Considere a Figura 12.63 e elabore um problema para ajudar outros estudantes a entender melhor os sistemas trifásicos não equilibrados.