Análise Nodal
Teoria
Continue aqui e aprenda análise nodal da melhor maneira e arrase na sua prova!
A análise nodal, ou conhecida as vezes como tensão de análise de um nó, é um método para determinar a tensão, ou diferença de potencial, entre "nós" em um circuito elétrico.
Eu vou te ensinar agora, com um passo a passo, a como fazer essa análise para 2 casos distintos.
Análise Nodal SEM fonte de tensão
Considere esse circuito elétrico abaixo:
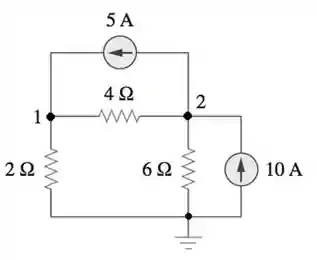
Para encontrarmos as tensões em cada nó vamos seguir o passo a passo:
Passo 1
Identificar os nós do circuito e nomear as tensões associadas a cada um deles.
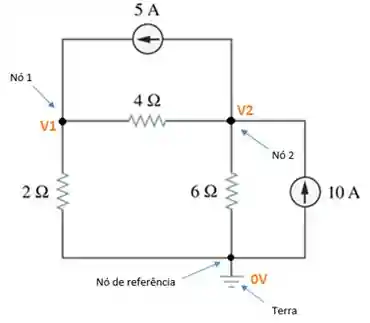
Obs.: Escolhemos o nó da terra (aqueles 3 tracinhos ali embaixo) como o nó de referência e ele tem potencial igual a
Passo 2
Escolher o sentido das correntes.
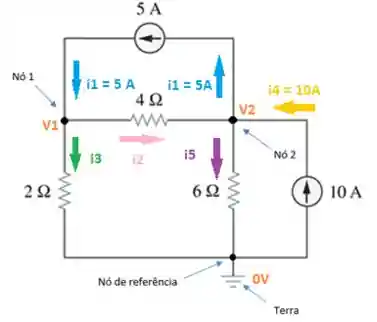
Obs.: Aqui nesse caso a gente escolhe um sentido para corrente porque não tem um fonte de tensão. Podemos escolher o sentido que quisermos, se o sentido não for o real da corrente, o valor será negativo. Fica tranquilo. Mas, quando tiver uma fonte de tensão vamos respeitar o sentido da corrente imposto por ela, ok?
Passo 3
Aplicar a Lei de Kirchhoff das Correntes (LKC) em cada nó (excluindo o nó da terra)
Nó 1
Nó 2
Montando um sistema com essas duas equações, temos:
Passo 4
Utilizar a Lei de Ohm para escrever a corrente em função da tensão de cada nó.
Passo 5
Agora basta a gente substituir as expressões para correntes no passo 4 no sistema encontrado no passo 3 e resolver o sistema que ficaá todo em função de
E prontinho, encontramos as tensões em cada nó!
Análise Nodal COM fonte de tensão
Aqui nós podemos separar em dois casos:
CASO 1: A fonte de tensão está conectada entre um nó e o terra, fazendo com que a tensão no nó seja igual a tensão da fonte.
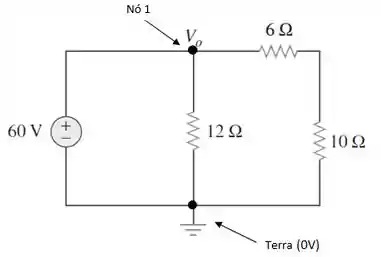
Nesse caso, não há nenhuma conta a ser feita. No circuito acima, a fonte de tensão de
CASO 2: Quando a fonte de tensão está conectada entre dois nós, sendo que nenhum deles é de referência (terra), isso forma o chamado SUPERNÓ.
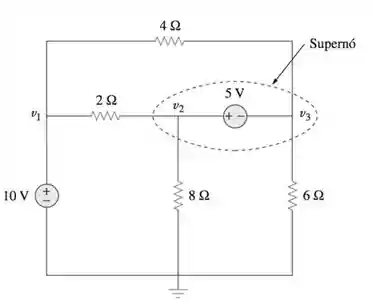
Nesse caso, para o supernó teremos uma informação a mais: a diferença entre as tensões nos nós será igual a tensão na fonte.
Agora, o passo a passo será bem semelhante ao que vimos para sos circuitos sem fonte de tensão.
Vamos aplicar o passo a passo nesse último circuito aí.
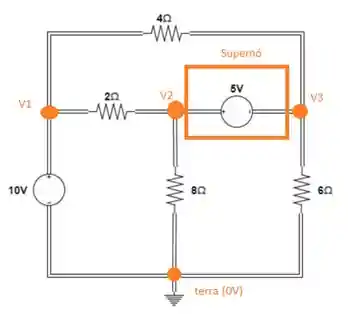
Passo 1
Identificar os nós e nomear tensões.
Passo 2
Identificar o sentido das correntes.
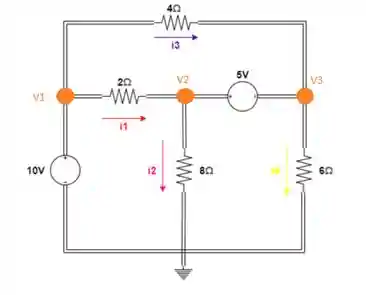
Lembrando que agora precisamos obedecer o sentido das correntes imposto pelas fontes de tensão, beleza?
Passo 3
Aplicar LCK para o supernó, embrando que encaramos o surpernó como uma coisa só (não olhamos o nó 2 e nó 3 separadamente).
Passo 4
Escrever as correntes em função das tensões usando a Lei de Ohm e substituir na equação do passo 3.
Obs.: Nesse ponto, é importante percebermos que
E, usaremos a informação a mais que o supernó nos fornece para termos uma segunda equação aqui e conseguirmos montar um sistema:
Passo 5
Nosso último passo é resolver o sistema e pronto!
Conseguiu pega a dinâmica?
É importante fazer bastante exercícios pra ficar expert! 😉
Análise Nodal COM fonte de tensão
Exercícios Resolvidos
Exercício Resolvido #1
Livro Sadiku, p.100, Problema 3.3
Determine as correntes e a tensão .
Passo 1
Nesse exercício, a tensão nodal e as correntes já foram nomeadas. Como os elementos de cada ramo estão ligados em paralelo, cada nó do circuito terá o mesmo potencial , já que toda parte inferior do circuito está ligada ao terra, e, portanto, o potencial é conhecido (0 volts).
Passo 2
Então a primeira coisa a ser feita, é aplicar a famosa LCK para os nós.
Passo 3
Agora vamos escrever as correntes em função da tensão nodal :
Passo 4
Substituindo as correntes na primeira equação, temos que:
Encontrando :
Passo 5
Para terminar, vamos substituir o valor encontrado de nas equações das correntes:
Resposta
Exercício Resolvido #2
Livro Sadiku, 5ª edição, p.75, Problema prático 3.1
Calcule as tensões nodais no circuito mostrado na Figura abaixo.
Passo 1
A primeira coisa a ser feita nesse método é analisar quantos nós se tem no circuito. No circuito acima existem 3 nós, sendo que os nós 1 e 2 possuem tensões desconhecidas que o exercício pede para calcular. O terceiro nó está localizado junto à terra, e, portanto, o potencial é conhecido (0 volts).
Passo 2
Agora vamos desenhar os sentidos das correntes de cada ramo do circuito e nomear as tensões de cada nó para podermos aplicar a LKC.
Equações de corrente para o nós:
Passo 3
Achar as equações das correntes em relação às tensões em cada resistor:
Passo 4
Substituindo as correntes nas duas primeiras equações, temos que:
Simplificando:
Agora teremos que resolver esse sistema aí de cima. Há vários jeitos de resolvê-lo, mas vamos fazer assim:
Passo 5
Primeiro vamos multiplicar a primeira equação por (-13) e o resultado somaremos com a segunda:
Em seguida, substituiremos o valor encontrado de na segunda equação:
Prontinho, só sucesso!
Resposta
Exercício Resolvido #3
Introdução à análise de circuitos – Robert L. Boylestad – Ed. 12 – Exercício 8.40 Adaptada
Escreva as equações nodais usando a abordagem geral para o circuito da figura e resolva:
Passo 1
Primeiro, vamos identificar os nós e o terra:
Passo 2
Vamos identificar as correntes que entram e saem dos nós A e B:
Como vimos que as fontes de corrente estão direcionando as correntes e para entrar no nó de terra, vamos direcionar as correntes e saindo do nó de referência, pois como sabemos a soma das correntes que entram no nó deve ser igual a soma das correntes que saem do nó.
No caso da corrente , escolhemos a corrente no sentido que desejamos.
Passo 3
Através da LKC, as equações para cada nó são:
Nó A:
Pela Lei de Ohm, sabemos que a corrente é igual a tensão em cima do resistor dividido pelo valor da resistência:
No caso da corrente saindo de um nó e entrando em outro, devemos colocar que a tensão é a diferença das tensões do nó de saída da corrente e a tensão do nó de entrada da corrente:
Logo, substituindo na equação :
Nó B:
Passo 4
Encontramos então o sistema:
Subtraindo da primeira equação a segunda equação:
Multiplicando tudo por 4:
Passo 5
Substituindo na primeira equação:
Multiplicando tudo por 8:
Passo 6
Substituindo na seguinte equação:
Ai já encontramos as tensões nodais que era desde o início o nosso objetivo!
Resposta
Exercício Resolvido #4
Livro Sadiku, 5ª edição, p.101, Problema 3.5
Obtenha no circuito a figura abaixo:
Passo 1
Vamos com calma. No circuito acima, temos apenas dois nós:
Escolhendo o nó 2 como referência, fazemos com que a tensão no nó 1 seja o próprio potencial , já que o circuito é paralelo. Além disso, vamos escolher os sentidos das correntes:
Aplicando a LKC no nó 1:
Passo 2
Agora vamos escrever nossas correntes em função da tensão no nó:
Isolando as correntes:
Passo 3
Substituindo as correntes:
Simplificando e isolando :
Resposta
Exercício Resolvido #5
Livro Sadiku, p.101, Problema 3.10
Determine e as tensões nodais:
Passo 1
Vamos começar! No circuito acima existem 4 nós.
Agora, vamos escolher o nó 4 como o terra, nomear as tensões de cada nó e desenhar os sentidos das correntes de cada ramo do circuito para podermos aplicar a LCK.
Passo 2
Equações de corrente para os nós:
Passo 3
Achar as equações das correntes em relação às tensões em cada resistor:
Passo 4
Agora vamos substituir no sistema de 3 equações aquelas encontradas para cada corrente:
Simplificando:
Passo 5
Agora teremos que resolver esse sistema aí de cima. Primeiro vamos substituir por na primeira equação:
Como, :
Substituindo o valor encontrado de na segunda equação:
Passo 6
Para terminar, falta encontrarmos o valor de :
Resposta
Exercício Resolvido #6
Livro Sadiku, 5ª edição, p.101, Problema 3.11
Determinar
Passo 1
Queremos encontrar a tensão nodal que se encontra no nó 1, pois já sabemos o potencial do nó 2, que é o terra (0 volts). Para isso, vamos desenhar os sentidos das correntes de cada ramo do circuito e aplicar a LCK.
Equação de corrente para o nó 1:
Passo 2
Agora vamos escrever nossas correntes em função da tensão nodal:
Se ficar na dúvida, é só aplicar a lei das tensões de Kirchhoff, por exemplo, na malha da direita:
Passo 3
Substituindo na primeira equação:
Simplificando:
Resposta
Exercício Resolvido #7
Livro Sadiku, 5ª edição, p.101, Problema 3.12
Determine .
Passo 1
No circuito abaixo, os nós 1 e 2 possuem tensões desconhecias, já que o terceiro está ligado ao terra.
Passo 2
Agora vamos desenhar os sentidos das correntes de cada ramo do circuito e nomear as tensões de cada nó para podermos aplicar a lei das correntes de Kirchhoff.
Além disso, a tensão nodal tem própria tensão que se pede no exercício.
Equações de corrente para o nós:
Passo 3
Achar as equações das correntes em relação às tensões nodais:
Passo 4
Substituindo as correntes nas equações de corrente de cada nó:
Simplificando:
Passo 5
Isolando na segunda equação e substituindo na outra, temos:
Pronto!
Resposta
Exercício Resolvido #8
Livro Sadiku, 5ª edição, p.102. Problema 3.14
Usando análise nodal, determine no circuito abaixo:
Passo 1
Bora lá! No circuito acima, temos apenas 3 nós.
Escolhendo o nó 3 como referência (terra), fazemos com que a tensão no nó 2 seja o próprio potencial . Além disso, vamos escolher os sentidos das corretes e nomear a tensão do nó 1:
Passo 2
Aplicando a LCK, temos as seguintes equações de corrente para o nós:
Passo 3
Achar as equações das correntes em relação às tensões nodais:
Passo 4
Substituindo as correntes nas duas primeiras equações, temos que:
Simplificando:
Passo 5
Agora teremos que resolver esse sistema aí de cima. Primeiro vamos isolar na primeira equação:
Em seguida, substituir na segunda equação:
Resposta
Exercício Resolvido #9
Livro Sadiku, 5ª edição, p.79, Problema prático 3.3
Calcular e no circuito abaixo:
Passo 1
No circuito acima, ao escolhermos o nó inferior como referência, teremos uma fonte de tensão entre dois nós, formando um supernó. Não se preocupe, vamos com calma.
Passo 2
Primeiro, vamos escolher os sentidos das corretes e nomear as tensões de cada nó para aplicarmos a LCK:
Aplicando a LCK ao supernó, temos a seguinte equação:
Passo 3
Achar as equações das correntes em relação às tensões nodais:
Passo 4
Substituindo as correntes na primeira equação, teremos que:
Simplificando:
Passo 5
Temos duas incógnitas e apenas uma equação. Precisamos encontrar uma outra equação que relacione e .
Para isso, vamos aplicar a lei das tensões de Kirchhoff para o supernó:
Percorrendo o laço:
Passo 6
Pronto, agora que temos duas equações para as duas incógnitas, vamos resolver esse sistema aí de baixo:
Primeiro vamos isolar na segunda equação:
Em seguida, substituir na primeira equação:
Logo:
Então, se liga! Sempre que aparecer um supernó é esse o procedimento: Aplicar a LCK e a LTK!
Passo 7
Agora, para terminar, precisamos encontrar :
Resposta
Exercício Resolvido #10
Livro Sadiku, 5ª edição, p.102. Problema 3.18
Determine as tensões nodais no circuito abaixo:
Passo 1
No circuito acima, os nós já estão identificados. O nó inferior está ligado ao terra e entre os nós 1 e 3 temos uma fonte de tensão formando um supernó. Relaxa, vamos ver o que fazer para esse caso ;)
Passo 2
Primeiro, vamos escolher os sentidos das corretes e nomear as tensões de cada nó para aplicarmos a LCK:
Aplicando a LKC ao supernó, temos a seguinte equação de corrente:
Agora o mesmo para o nó 2:
Passo 3
Achar as equações das correntes em relação às tensões nodais:
Passo 4
Substituindo as correntes nas duas primeiras equações, temos que:
Simplificando:
Passo 5
Temos três incógnitas e apenas duas equações. Precisamos encontrar uma outra equação que relacione , e . Para isso, vamos aplicar a lei das tensões de Kirchhoff para o supernó:
Percorrendo o laço:
Passo 6
Pronto, agora que temos três equações para as três incógnitas, vamos resolver esse sistema aí de baixo:
Primeiro vamos isolar na terceira equação:
Em seguida, substituir na primeira equação:
Simplificando:
E agora na segunda:
Simplificando:
Passo 7
Agora, temos o seguinte sistema formado por essas duas novas equações:
Para resolver esse sistema vamos multipicar a segunda equação por (-4) e o resultado somaremos com a primeira:
Substituindo na segunda equação:
Passo 8
Calma, já está quase acabando, falta encontrarmos .
Sabemos que:
Substituindo o valor encontrado para :
Ufa! Acabou!