Princípio Da Superposição
Produzido por Alexandre NunesTeoria
Fala aí! Hoje vamos falar sobre Princípio da Superposição.
Esse é um tema muito recorrente em várias áreas de matemática ou física, mas aqui vamos focar em sua aplicação para circuitos elétricos, beleza?
Então bora lá aprender como funciona esse negócio, com um montão de exercícios resolvidos só pra você 😋
⭐ Veja também ⭐
O que diz o Princípio da Superposição?
De uma maneira geral, o Princípio da Superposição se aplica sempre que as contribuições de partes individuais podem ser somadas linearmente para se obter uma contribuição total.
Quando aprendermos a aplicar o Princípio para circuitos, vamos encontrar um jeito de reduzir circuitos complexos em outros bem mais simples. Mas antes, a gente precisa entender se esses circuitos se comportam de maneira linear, pra sabermos se a tal da superposição realmente pode ser aplicada!
Princípio da Linearidade
Olha só uma maneira bem tranquila de entender a linearidade de um circuito. Vou te mostrar por meio de um exemplo 👇
Exemplo: No circuito abaixo, calcule
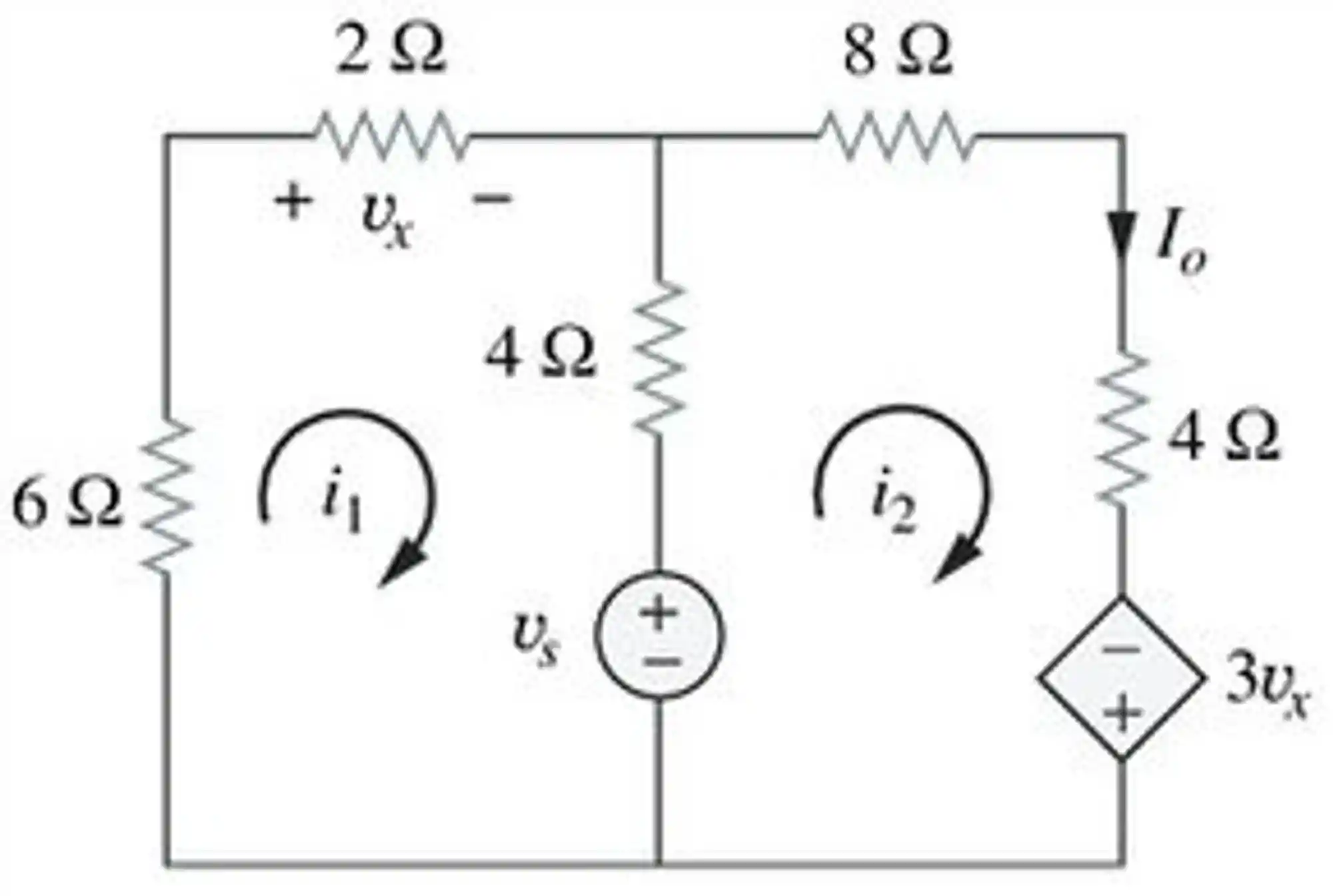
Vamos começar com uma análise de malha pela Lei de Kirchhoff para tensões.
Para a malha 1:
Para a malha 2:
Só que pela lei de Ohm, a gente tira ali da primeira malha que
Aí a gente chega no seguinte sistema:
Só resolver isso aí. Somando as duas equações:
Agora substituindo isso na equação (1):
Ahh, você pode substituir tanto na equação (1) quanto na equação (2), bele? Vai dar o mesmo resultado.
Olhando lá pro circuito, a gente percebe que
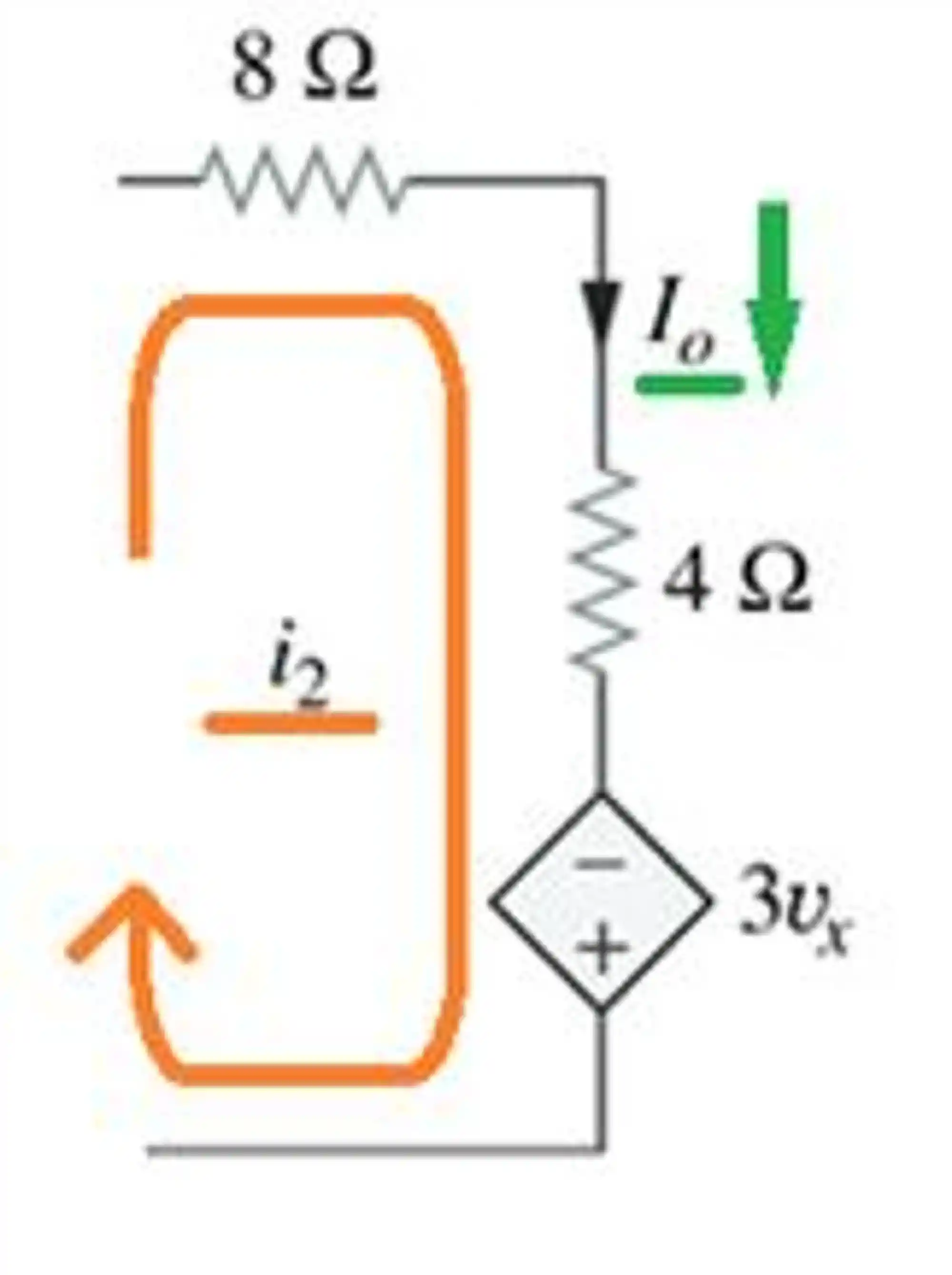
Então, quando
E quando
Percebeu uma coisa? O valor da tensão foi dobrado e a corrente também foi. Isso quer dizer que elas apresentam uma relação linear.
Então, em um circuito linear, a saída é linearmente dependente da entrada. Por exemplo, se
Tudo isso foi só pra te mostrar por que o Princípio da Superposição vai ser válido. Agora, vamos ver como aplicá-lo de fato!
Como usar o Princípio da Superposição
Com o princípio da superposição, a gente calcula individualmente a contribuição de cada fonte e depois soma os resultados.
Pra entender como se faz isso, você pode assistir esse vídeo aqui com tudo bem explicadinho, ou então me acompanhar no texto logo abaixo que já te conto tudo 👇😉
Para aplicar o Princípio, precisamos fazer algumas considerações:
👉 Temos que considerar uma fonte independente de cada vez. Para isso, precisamos desligar as outras. Isso quer dizer que:
- Cada fonte de tensão deve ser substituída por 0 (curto-circuito).
- Cada fonte de corrente deve ser substituída por 0 (circuito aberto).
- As fontes dependentes ficam intactas.
Vou te explicar como funciona esse negócio com mais um exercício resolvido.
Exemplo: Encontre a tensão v no circuito abaixo usando superposição.
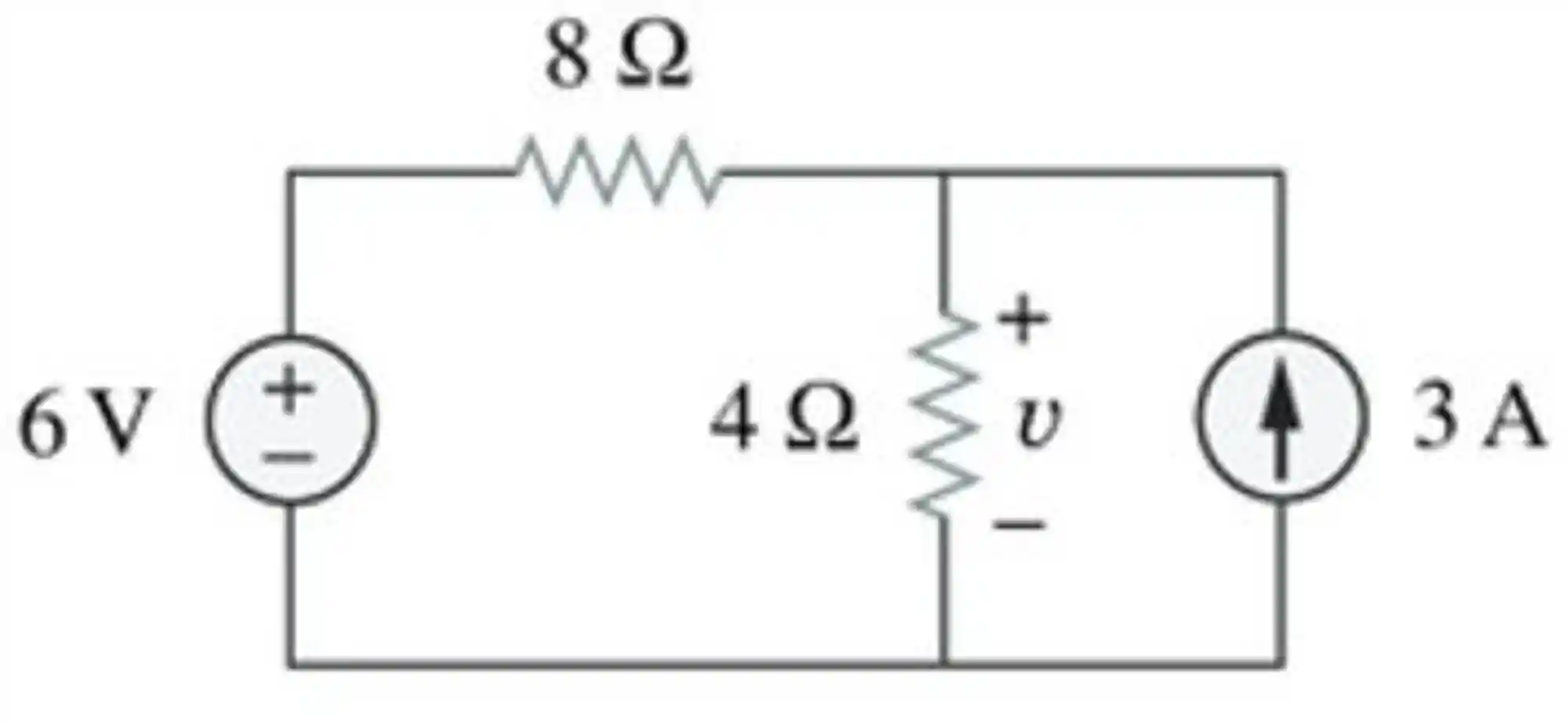
Repare que esse circuito tem duas fontes independentes (6 V e 3 A). Então, a tensão v vai ser a soma das contribuições de tensão das duas fontes individualmente!
Vamos começar calculando
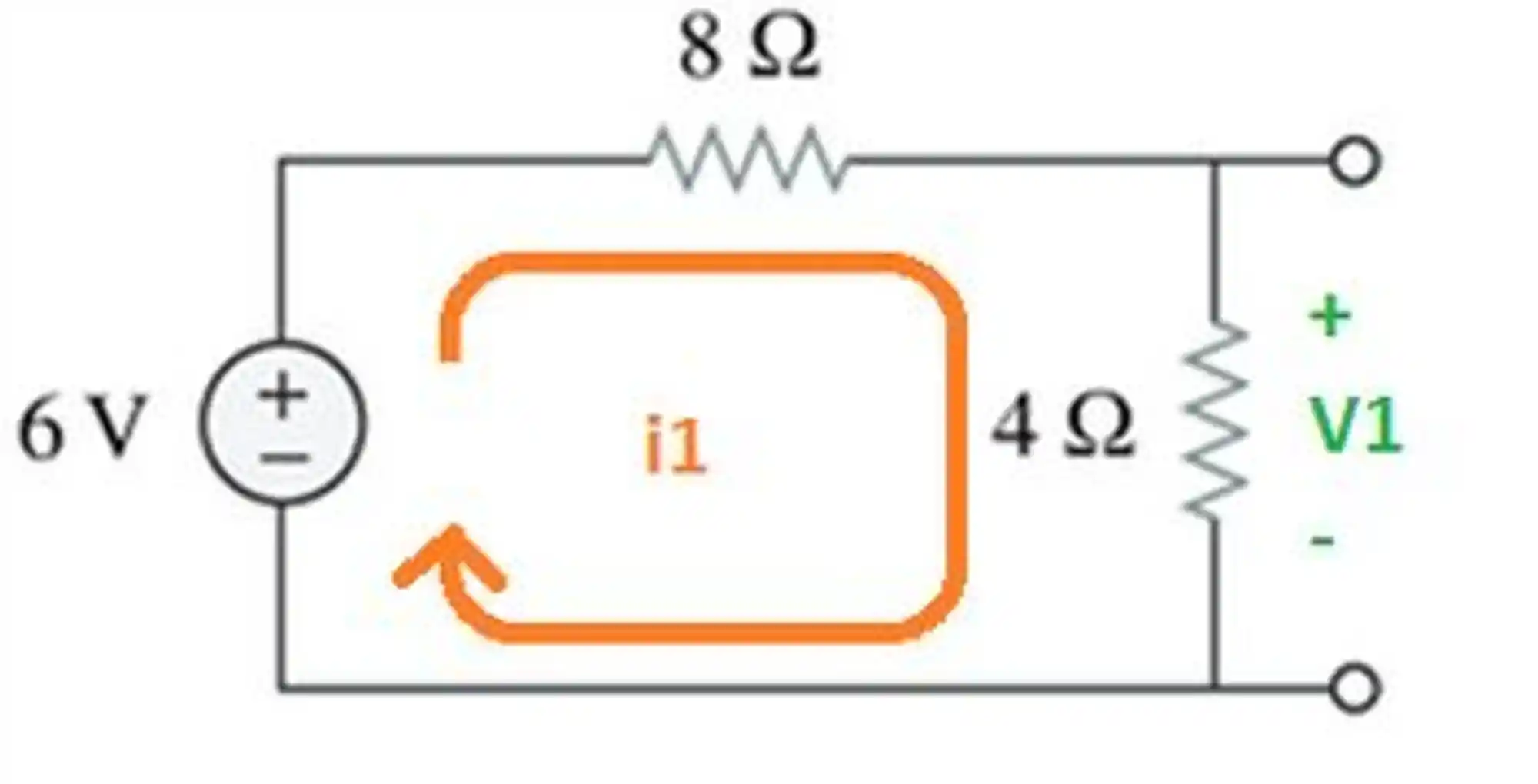
Para isso, desligamos a fonte de corrente de 3 A e aplicamos a lei de Kirchhoff:
E pela lei de Ohm, a tensão no resistor de
Agora fazemos o contrário. Vamos desligar a fonte de tensão 6 V para calcular a contribuição da fonte de corrente.
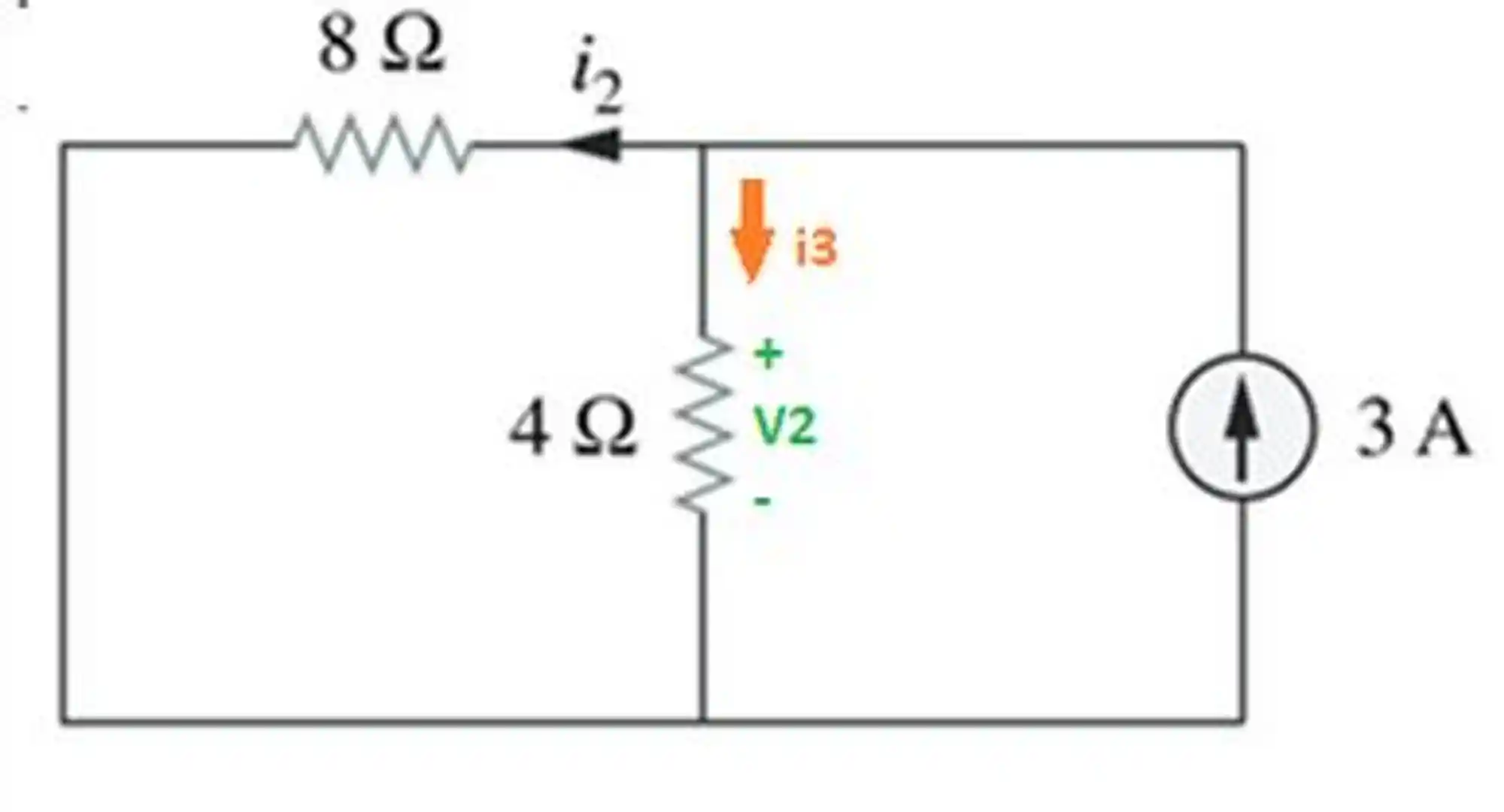
Vamos usar divisor de corrente para encontrar aquele
E pela lei de Ohm:
Beleza! Agora é só somar os dois resultados que encontramos:
Molezinha, né? Bora praticar mais um pouquinho com mais alguns exercícios resolvidos passo a passo!
Exemplo: Encontre a tensão v no circuito abaixo usando superposição.
Exercícios Resolvidos
Exercício Resolvido #1
Livro Sadiku, 5ª edição, p.114, problema prático 4.1
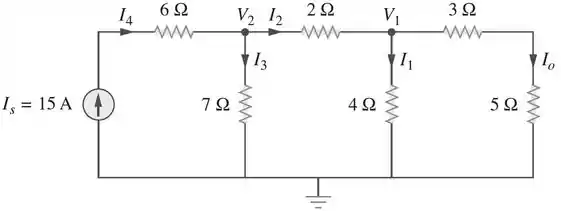
Para o circuito abaixo, determine quando e :
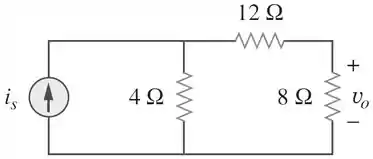
Passo 1
Antes da gente começar a usar a Superposição, precisamos entender bem essa ferramenta poderosa que se chama Linearidade! Então vamos esquentar nossos motores com essa questão que é bem simples.
Nessa questão precisamos achar uma relação entre e , para verificarmos a relação de linearidade do circuito.
Passo 2
Para isso, vamos utilizar o método de análise nodal:
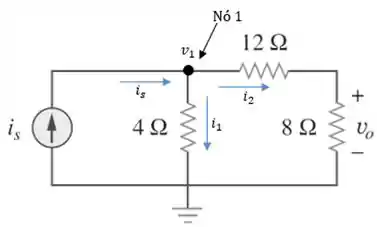
Aplicando LCK no nó 1, a equação das correntes fica assim:
Passo 3
Escrevendo as correntes em função da tensão nodal :
Passo 4
Substituindo na equação das corretes:
Passo 5
Agora, vamos utilizar divisor de tensão para calcular a tensão :
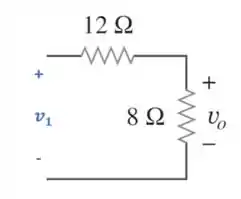
Substituindo :
Passo 6
Quando , temos:
Quando , temos:
Esses resultados comprovam a relação de linearidade, pois quando a fonte de corrente teve seu valor multiplicado por , o também foi multiplicado pelo mesmo valor.
Resposta
e
Exercício Resolvido #2
Livro Sadiku, 5ª edição, p.115, problema prático 4.2
Supondo , use a propriedade da linearidade para calcular o valor real de no circuito abaixo:
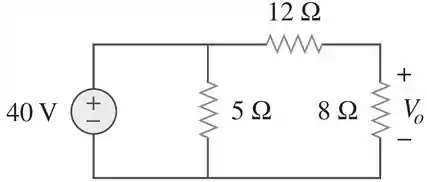
Passo 1
Nesse problema ele quer saber quanto de tensão a fonte tem que fornecer para que no resistor de consiga “chegar” 1V. Sendo assim, vamos encontrar o valor de entrada da fonte de tensão que produz essa saída, conforme o esquema abaixo:
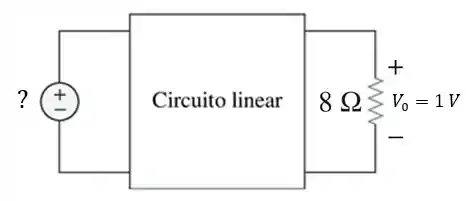
Passo 2
Pela lei de Ohm:
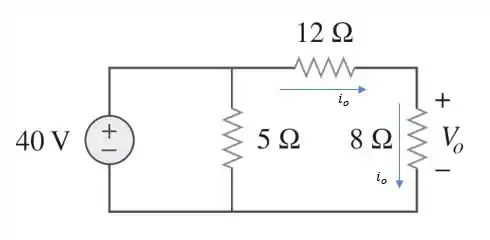
Passo 3
Como os resistores de 12Ω e 8 estão em série, a tensão nodal será:
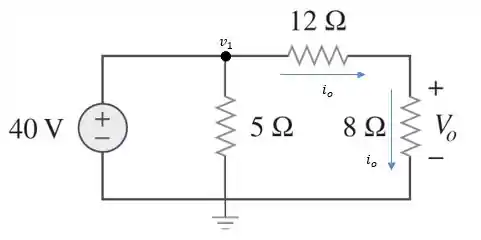
Como a tensão nodal está em paralelo com a fonte de tensão, o valor da fonte é o próprio .
Passo 4
Agora, vamos usar a propriedade da linearidade:
Quando , temos . Logo, quando valor da fonte de tensão for o real, ou seja, , então será:
Logo,
Resposta
Exercício Resolvido #3
Livro Sadiku, 5ª edição, p.115, exemplo 4.2
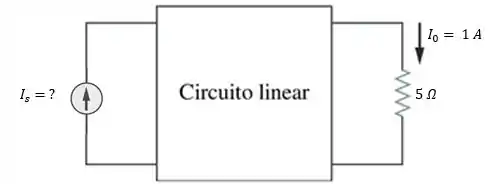
Supondo e usando a propriedade da linearidade, encontre o valor real de no circuito abaixo:
Passo 1
Nesse problema ele quer saber quanto de corrente a fonte tem que fornecer para que no resistor de consiga “chegar” 1A. Sendo assim, vamos encontrar o valor de entrada da fonte de corrente que produz essa saída, conforme o esquema abaixo:
Passo 2
Como circuito já está preparado para ser feito por análise nodal:
Se :
Como :
Passo 3
Aplicando LCK no nó de :
Substituindo:
Como,
Substituindo: e :
Passo 4
Como tem-se que:
Substituindo :
Passo 5
Agora, vamos aplicar a LCK no nó de :
Substituindo:
Como é o próprio :
Isso mostra que supondo obteremos uma entrada . Logo, utilizando a propriedade da linearidade, quando a entrada for o valor real da fonte de corrente, ou seja, , a saída resultará no valor real de .
Multiplicando por três:
Resposta
Exercício Resolvido #4
Livro Sadiku, 5ª edição, p.117, problema prático 4.3
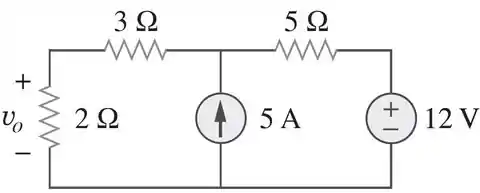
Usando o teorema da superposição, determine no circuito abaixo:
Passo 1
Precisamos encontrar utilizando o princípio da superposição. No circuito existem duas fontes independentes.
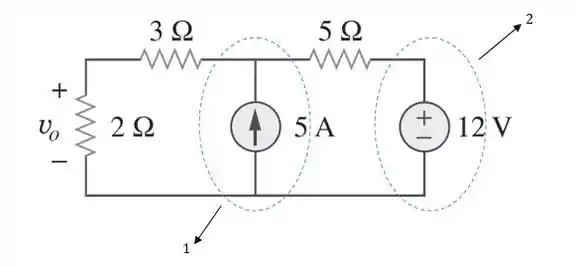
Logo, a tensão será a soma das contribuições de tensão das duas fontes individualmente, ou seja:
Passo 2
Primeiro, vamos determina . Para isso, vamos desconsiderar a fonte de tensão, ou seja, substituí-la por um curto-circuito:
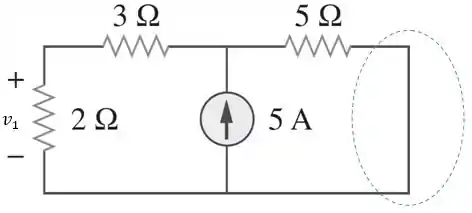
Passo 3
Agora, vamos calcular a contribuição da fonte de corrente de :
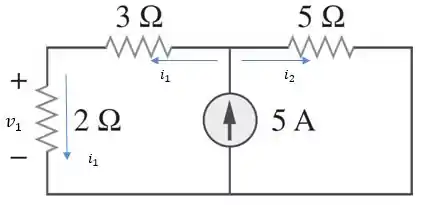
Usando divisor de corrente:
Logo, pela lei de Ohm:
Passo 4
Agora, precisamos calcular . Então, vamos desconsiderar a fonte de corrente, ou seja, substituí-la por um circuito aberto:
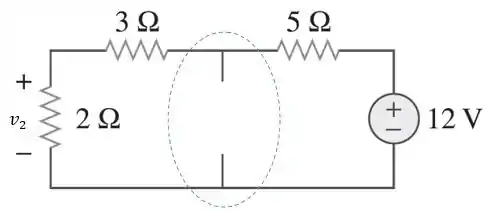
Como os resistores estão em série, vamos calcular a contribuição da fonte de utilizando divisor de tensão:
Passo 5
Para terminar, precisamos somar as contribuições de cada fonte:
Resposta
Exercício Resolvido #5
Introdução à análise de circuitos – Robert L. Boylestad – Ed. 12 – Exercício 9.4
Usando a superposição, calcule a corrente através da fonte de 24Vna figura:
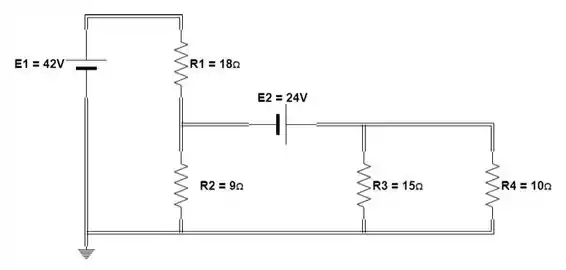
Passo 1
Primeiro vamos analisar o efeito da fonte de tensão , para isso vamos substituir a fonte de tensão por um curto circuito:
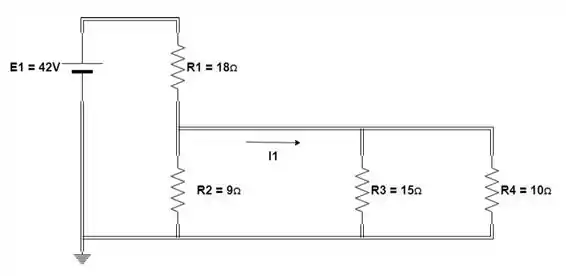
Passo 2
Vamos fazer a resistência equivalente entre e :
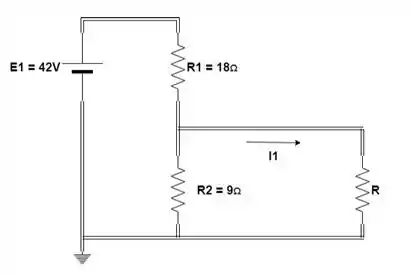
Passo 3
Para calcular a corrente total, devemos fazer a resistência equivalente do circuito completo.
Primeiro está em paralelo com :
Depois, essa resistência está em série com :
A corrente total será:
Passo 4
Podemos perceber que essa corrente total se divide entre os resistores e :
Passo 5
Agora vamos analisar o efeito da fonte de tensão , para isso vamos substituir a fonte de tensão por um curto circuito:
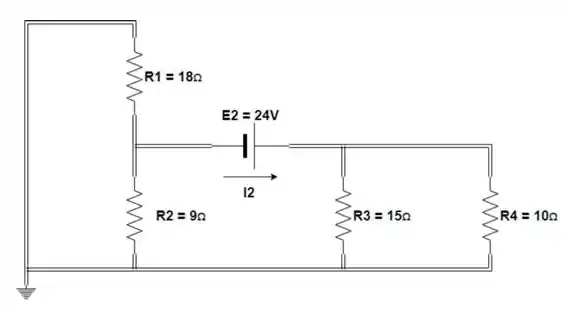
Passo 6
Para calcular a corrente que passa pela fonte de 24V, devemos calcular a corrente total que sai da fonte e circula pelos resistores.
Primeiro, vamos calcular a resistência total. Inicialmente percebemos que os resistores e estão em paralelo, assim como os resistores e .
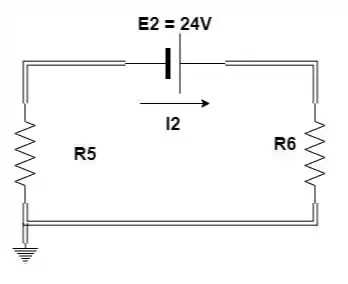
Passo 7
Assim, a corrente total será:
Resposta
A corrente que passa pela fonte de 24V será igual a 3,16A.
Exercício Resolvido #6
Introdução à análise de circuitos – Robert L. Boylestad – Ed. 12 – Exercício 9.5
Usando a superposição, calcule a tensão para o circuito na figura:
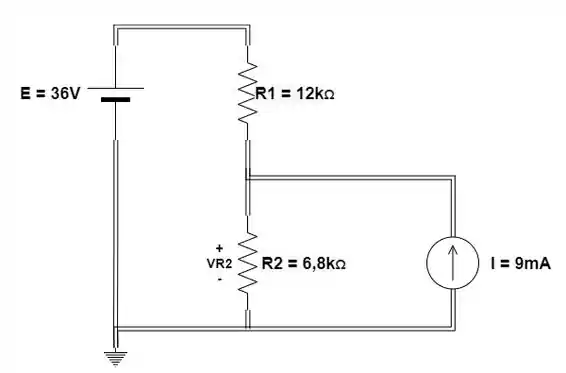
Passo 1
O primeiro passo é analisar o efeito da fonte de tensão , enquanto substituímos a fonte de corrente por um circuito aberto.
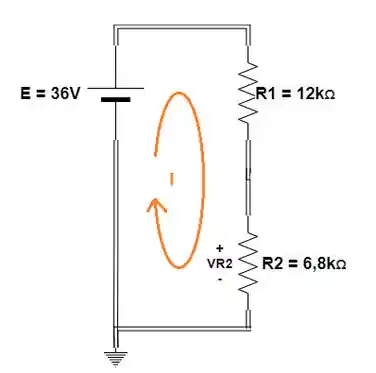
Percebemos que circula uma corrente que gera a queda de tensão , podemos encontrar através do divisor de tensão:
Passo 2
O segundo passo é analisar o efeito da fonte de corrente I, enquanto substituímos a fonte de tensão por um curto circuito.
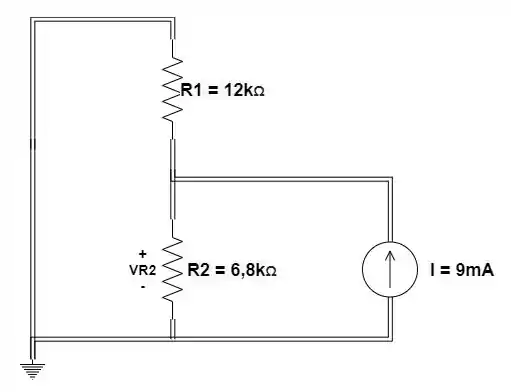
Passo 3
Devemos realizar o divisor de corrente entre os resistores e :
Para calcular :
Passo 4
Somando as duas contribuições, uma da fonte de tensão e outra da fonte de corrente:
Resposta
Exercício Resolvido #7
Introdução à análise de circuitos – Robert L. Boylestad – Ed. 12 – Exercício 9.6
Usando a superposição, calcule a a corrente através de para o circuito na figura:
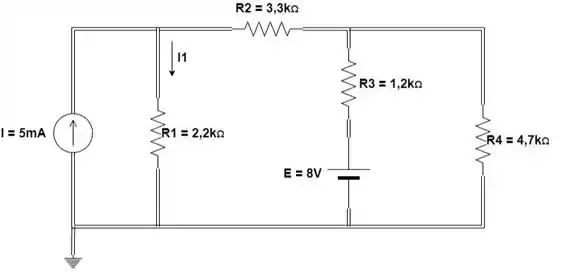
Passo 1
Primeiro vamos analisar o efeito da fonte de tensão , enquanto substituímos a fonte de corrente por um circuito aberto:
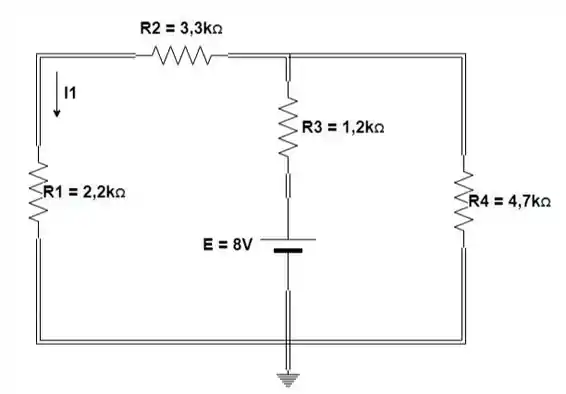
Passo 2
Para encontrar , vamos calcular a resistência equivalente total. Vamos que está em série com :
Essa resistência está me paralelo com :
Essa nova resistência está em série com :
Passo 3
A corrente total é igual a:
Para encontrar devemos realizar um divisor de corrente:
Passo 4
Depois vamos analisar o efeito da fonte de corrente substituindo a fonte de tensão por um curto circuito:
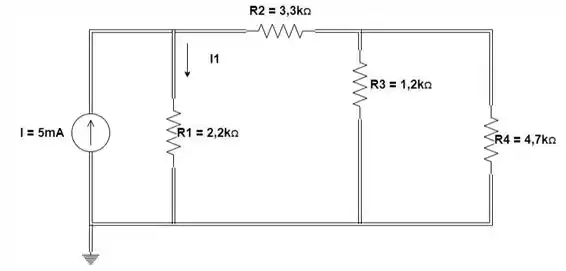
Passo 5
Devemos calcular novamente a resistência equivalente entre os resistores :
em paralelo com :
Essa resistência em série com :
Passo 6
Podemos realizar um divisor de corrente entre os resistores e :
Passo 7
Vamos somar as duas correntes que compõem a corrente :
Resposta
Exercício Resolvido #8
Livro Sadiku, 5ª edição, p.118, problema prático 4.4
Use superposição para determine no circuito abaixo:
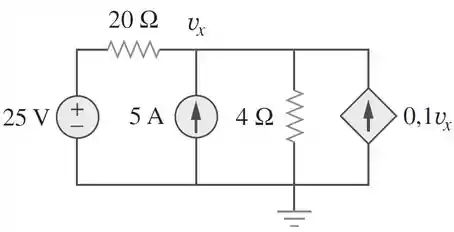
Passo 1
Precisamos encontrar utilizando o princípio da superposição. No circuito existem duas fontes independentes e uma dependente.
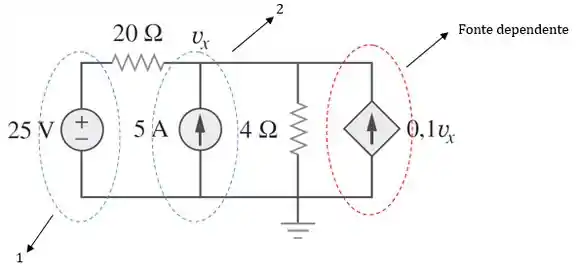
Logo, a tensão será a soma das contribuições de tensão das duas fontes independentes individualmente, ou seja:
Passo 2
Primeiro, vamos determina . Para isso, vamos desconsiderar a fonte de corrente, ou seja, substituí-la por um circuito aberto, lembrando que a gente deixa a fonte dependente intacta:
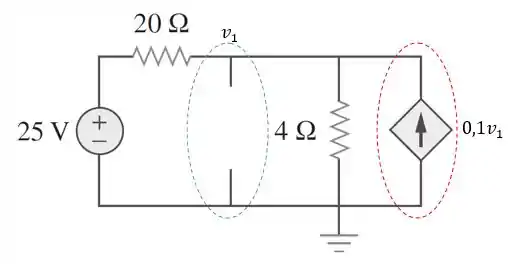
Passo 3
Agora, vamos calcular a contribuição da fonte de tensão de :
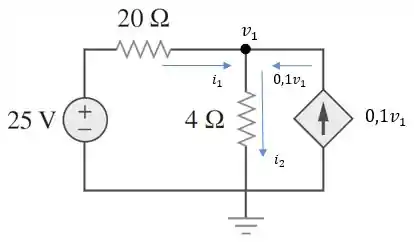
Para isso, vamos usar análise nodal. Aplicando a LCK no nó de :
Passo 4
Agora, vamos escrever as correntes em função da tensão nodal
Passo 5
Substituindo na equação das correntes do nó:
Passo 6
Agora, precisamos calcular . Então, vamos desconsiderar a fonte de tensão, ou seja, substituí-la por um curto-circuito, sempre lembrando que deixamos a fonte independente da mesma forma:
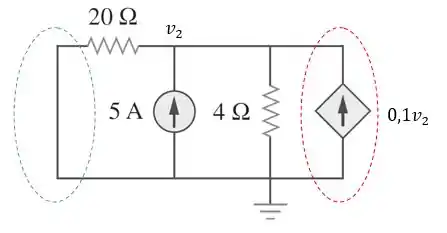
Passo 7
Vamos ajeitar os elementos para melhorar a visualização e aplicar análise nodal novamente:
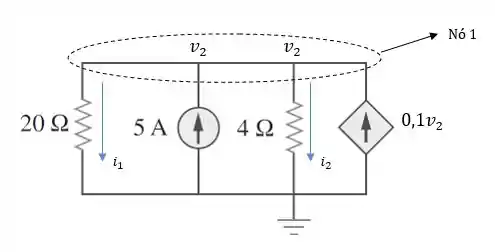
Aplicando LCK no nó 1:
Passo 8
Escrevendo as correntes em função da tensão nodal :
Passo 9
Substituindo na equação das correntes do nó:
Passo 10
Ufa! Para terminar, precisamos somar as contribuições de cada fonte:
Resposta
Exercício Resolvido #9
Livro Sadiku, 5ª edição, p.119, problema prático 4.5
Determine no circuito abaixo usando o princípio da superposição.
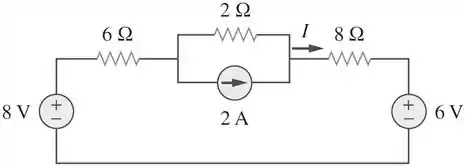
Passo 1
Precisamos encontrar utilizando o princípio da superposição. No circuito existem três fontes independentes.
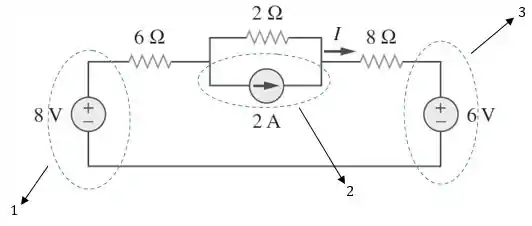
Logo, a corrente será a soma das contribuições de corrente das três fontes individualmente, ou seja:
Passo 2
Primeiro, vamos determina . Para isso, vamos desligar a fonte de tensão de , substituindo por um curto-circuito e a de corrente de , substituindo por um circuito aberto:
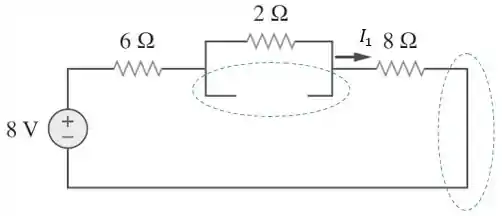
Passo 3
Vamos ajeitar o circuito e calcular a contribuição da fonte de tensão de :
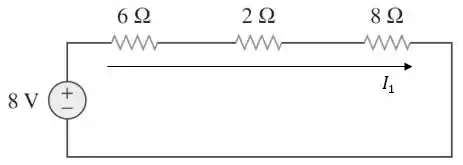
Aplicando a lei de Ohm:
Passo 4
Agora, precisamos calcular . Então, vamos desligar as duas fontes de tensão, ou seja, substituí-las por um curto-circuito:
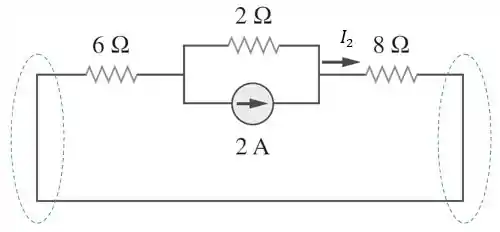
Passo 5
Vamos dar uma ajeitada no circuito para entendermos melhor o que fazer:
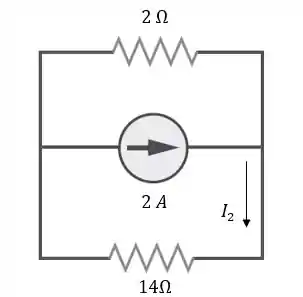
Usando divisor de corrente:
Passo 6
Falta determinarmos . Para isso, vamos desligar a fonte de tensão de , substituindo por um curto-circuito e a de corrente de , substituindo por um circuito aberto:
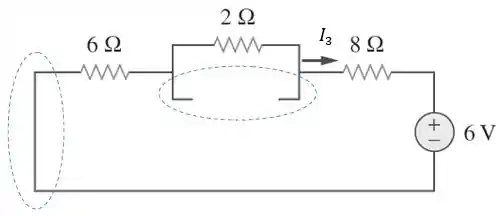
Passo 7
Agora, vamos ajeitar o circuito e calcular a contribuição da fonte de tensão de :
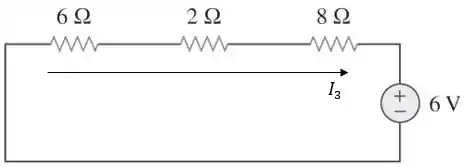
Aplicando a lei de Ohm:
Passo 8
Para terminar, precisamos somar as contribuições de cada fonte:
Substituindo:
Resposta
Exercício Resolvido #10
Livro Sadiku, 5ª edição, p.145, problema 4.19
Use superposição para determinar no circuito abaixo.
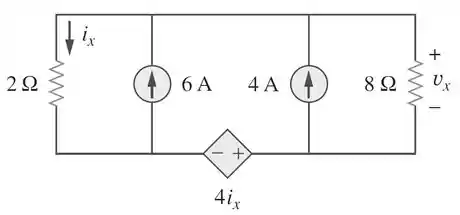
Passo 1
Precisamos encontrar utilizando o princípio da superposição. No circuito existem duas fontes independentes de corrente e uma fonte dependente de tensão.
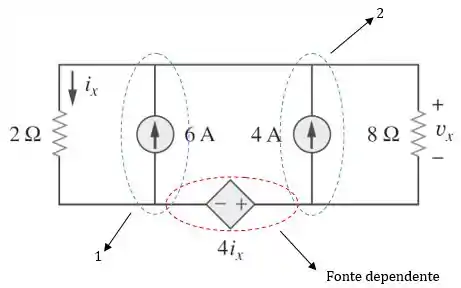
Logo, a tensão será a soma das contribuições de tensão das duas fontes independentes individualmente, ou seja:
Passo 2
Primeiro, vamos determina . Para isso, vamos desligar a fonte de corrente de , substituindo por um circuito aberto:
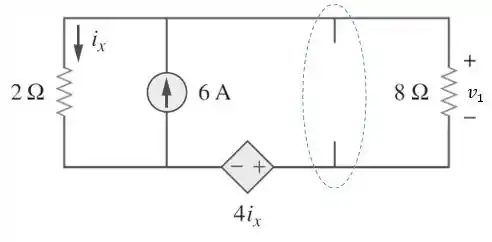
Passo 3
Vamos ajeitar o circuito e calcular a contribuição da fonte de tensão de , utilizando análise nodal.
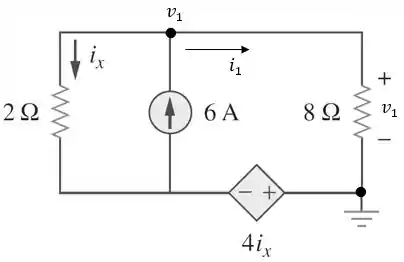
Aplicando a LCK no nó da tensão nodal :
Passo 4
Escrevendo as correntes em função da tensão nodal:
Substituindo na equação das correntes do nó:
Passo 5
Falta determinarmos . Para isso, vamos desligar a fonte de corrente de , substituindo por um circuito aberto.
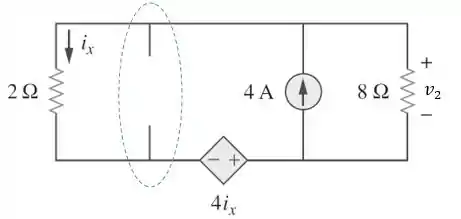
Passo 6
Agora, vamos ajeitar o circuito e calcular a contribuição da fonte de tensão de , utilizando análise nodal.
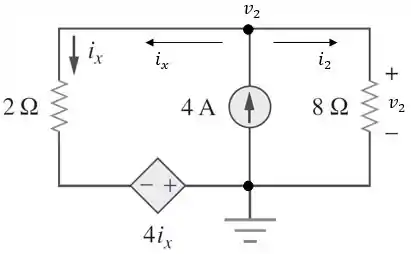
Aplicando a LCK no nó da tensão nodal :
Passo 7
Escrevendo as correntes em função da tensão nodal:
Substituindo na equação das correntes do nó:
Passo 8
Agora é somar as contribuições e correr para o abraço:
Substituindo: