Análise de malhas
Teoria
Fala aí, você caiu no Responde Aí! E agora vamos falar tudo sobre Análise de malhas
O básico sobre análise de malhas
A análise de malhas consiste em utilizar as Lei de Kirchhoff sobre uma malha para de encontrar as correntes desconhecidas de um circuito.
Mas é importante a gente ter dois conceitos bem definidos: o conceito de circuito planar e o conceito de malha
Circuito planar
Um circuito planar, é basicamente todo circuito que consegue ser representado sem que haja cruzamento de linhas.
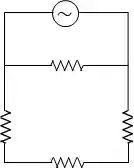
Porém tenha cuidado! As vezes um circuito pode parecer que tem linhas se cruzando, mas com um pouco de redesenho, percebemos que o circuito é planar:
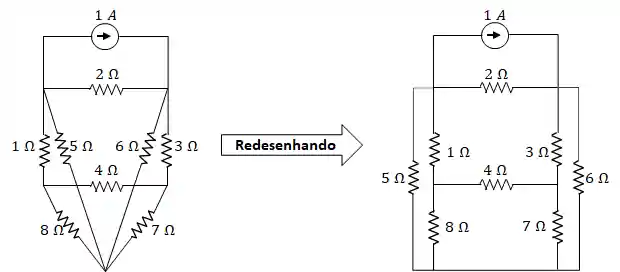
Malha
Malha é um laço no circuito, o qual não contém outro laço interno. Doido né? Calma, é simples. Olha o circuito abaixo, tem duas malhas.
Na figura acima, por exemplo, os caminhos
Ou seja, malhas são caminhos que começam e terminam no mesmo ponto, porém nesse caminho não pode existir uma rota alternativa.
Análise de malhas
Agora sim vamos falar da análise de malhas. Mas pra isso existem dois casos particulares: o primeiro caso é a análise de malhas SEM fonte de corrente e o segundo caso é a análise de malhas COM fonte de corrente
Malha SEM fonte de corrente
O primeiro caso que vamos estudar é quando não temos fonte de corrente na nossa malha. Para resolver questões assim seguimos os seguintes passos:
- Atribuir correntes de malha
, , , - Aplicar a Lei de Kirchhoff para Tensões em cada malha, para obter um sistema de equações
- Resolver o sistema de equações
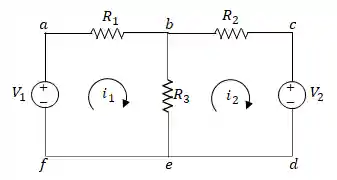
Exemplo Calcule as correntes sobre as malhas
Passo 1: Primeiro a gente define as correntes de cada malha
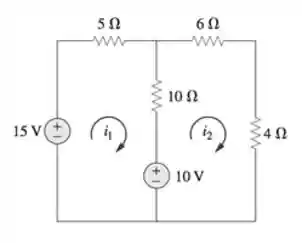
Passo 2: E agora vamos aplicar a Lei de Kirchhoff para Tensões, e montamos um sistema de equações:
Passo 3: Agora é só matemática! Vamos resolver as equações!
Primeiro vamos simplificar as equações:
Podemos dividir a primeira equação por
E somando as duas equações vamos ter que:
Logo:
Malha COM fonte de corrente
Agora, quando temos uma fonte de corrente a resolução fica ainda mais fácil!
Caso 1: Quando a fonte de corrente está em um ramo do circuito, o processo de resolução é igual ao anterior. Porém fica mais fácil, pois a corrente de malha é igual a corrente da fonte
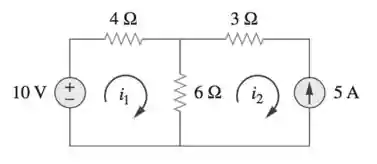
No casos como esse da imagem podemos afirmar sem sombra de dúvida que:
E pra definir a corrente
Caso 2: Quando temos uma fonte de corrente entre duas malhas a melhor forma é a gente trabalhar com a supermalha!
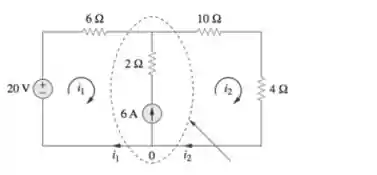
Uma supermalha é apenas o caminho que não passa pela fonte de corrente. Ou seja, é como se a gente ignorasse o caminho da fonte de corrente.
Pra resolver a gente faz o seguinte:
- Primeiro a gente cria uma supermalha ignorando o caminho da fonte de corrente.
- Depois aplicamos a Lei de Kirchhoff para Nós no caminho que foi ignorado no passo anterior
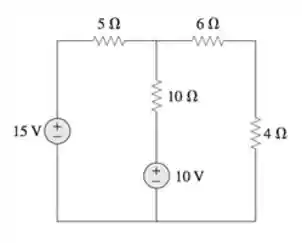
Exemplo: Calcule as correntes de malha
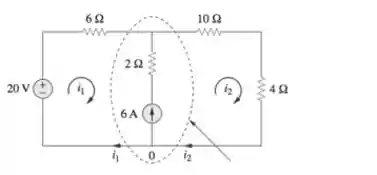
Passo 1: Vamos fingir que o caminho da fonte de corrente não existe e gerar uma equação:
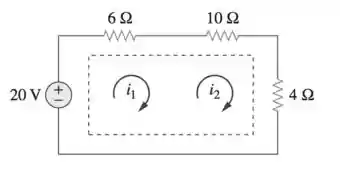
Passo 2: Agora vamos usar a Lei dos Nós no caminho da fonte de corrente para encontrar uma segunda equação:
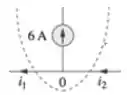
Observando o nó vemos que:
Passo 3: Pronto! Agora temos duas equações, vamos montar e resolver o sistema:
Aplicando a segunda equação na primeira temos:
Logo:
Videoaula
E pra ficar ainda mais ligado, da uma olhada nessa videoaula
E agora dá uma conferida nos exercícios pra praticar 👇
Análise de malhas
Videoaula
Exercícios Resolvidos
Exercício Resolvido #1
Livro Sadiku, p.107, Exercício 3.58
Determine , e no circuito da figura abaixo:
Passo 1
Primeira coisa a se fazer é LTK em cada malha, formando, assim, 3 equações:
Simplificando:
Passo 2
Isolando e das equações e :
Passo 3
Substituindo as equações do passo anterior em :
Passo 4
Substituindo o valor encontrado de nas equações e :
Resposta
Portanto,
Exercício Resolvido #2
Usando a análise de malhas, calcule e no circuito abaixo, se:
Passo 1
Vamos começar fazendo um LKT na malha 1 e 2 para achar e :
LKT na malha 1:
LKC na malha 2:
Passo 2
Como nós temos duas equações e duas incógnitas, podemos fazer um sistema e achar nossos resultados:
Multiplicando a primeira equação por e a segunda por ,
Somando as duas, chegamos em
Substituindo em qualquer uma das equações a gente acha o :
Resposta
Exercício Resolvido #3
Livro Sadiku, p.105, Exercício 3.36
Use a análise de malhas para determinar , e no circuito da figura abaixo.
Passo 1
Vamos escolher os sentidos das correntes de malha:
Passo 2
Agora vamos montar as equações de malha segundo a LTK:
Resolvendo por adição, vamos multiplicar a segunda linha por e a primeira por :
Passo 3
Substituindo o valor de na primeira equação:
Isolando :
Passo 4
Como:
Resposta
Exercício Resolvido #4
Introdução à análise de circuitos – Robert L. Boylestad – Ed. 12 – Exercício 8.23
Usando a abordagem geral para o método das malhas, determine a corrente através de cada resistor da figura:
Passo 1
Primeiro devemos desenhar o sentido das correntes em cada malha e nomear cada uma delas
Passo 2
Agora vamos marcar as polaridades das quedas de tensão produzidas em cada resistor pelas correntes que atravessam eles:
Passo 3
Pela LKT, podemos escrever a malha 1 como:
Pela LKT, podemos escrever a malha 2 como:
Passo 4
Pela equação 1, podemos definir que:
Substituindo na segunda equação:
Achamos que . Assim, .
Passo 5
Percebemos que a corrente que passa pelo resistor é a diferença entre as correntes e . Assim o sentido será definido pela maior corrente, nesse caso o sentido é o da corrente e o seu valor é:
Resposta
Exercício Resolvido #5
Livro Sadiku, p.107, Exercício 3.54
Determine as correntes de malha , e no circuito da figura abaixo:
Passo 1
Montar as equações de malha, segundo a LKT
Simplificando as equações:
Passo 2
Isolando e das equações e :
Passo 3
Substituindo as equações acima na equação :
Passo 4
Substituindo o valor encontrado acima nas equações isoladas de e :
Resposta
Exercício Resolvido #6
Livro Sadiku, p.106, Exercício 3.46
Calcule as correntes de malha e na figura abaixo:
Passo 1
Vamos analisar a primeira malha:
Temos que escrever as polaridades das quedas de tensão nos resistores, lembrando que como no resistor de 8Ω nós temos duas correntes passando por ele (, temos que considerar essas duas quedas na equação da primeira malha:
Logo, podemos escrever a equação da malha como:
Passo 2
Analisando a segunda malha:
Temos que escrever as polaridades das quedas de tensão nos resistores, lembrando que como no resistor de 8Ω nós temos duas correntes passando por ele (, temos que considerar essas duas quedas na equação da segunda malha:
Logo, podemos escrever a equação da malha como:
Passo 3
Reunindo as equações de malha segundo a LTK, temos:
Como:
Substituindo:
Passo 4
Agora, precisamos resolver esse sistema. Vamos fazer assim:
Primeiro, vamos isolar na segunda equação:
Substituindo na primeira:
Portanto, temos que:
Resposta
Exercício Resolvido #7
Introdução à análise de circuitos – Robert L. Boylestad – Ed. 12 – Exercício 8.31
Usando a abordagem da supermalha, calcule a corrente através de cada elemento do circuito:
Passo 1
Vamos definir as correntes que percorrem as malhas:
Passo 2
Agora vamos marcar as polaridades das quedas de tensão nos resistores.
Passo 3
Podemos verificar através das fontes de corrente que:
Vamos escrever a equação das malhas para a malha que só possui resistores e nenhuma fonte de corrente:
Passo 4
Vamos substituir a corrente por 8A e :
Assim, encontramos que:
Então:
Resposta
As correntes são:
Exercício Resolvido #8
Livro Sadiku, p.105, Exercício 3.44
Use análise de malhas para determinar no circuito da figura abaixo
Considerando a malha que contém a fonte de como a malha 1, a malha abaixo como a malha 2 e a malha da fonte de como a malha 3. As correntes , e , são pertencentes respectivamente as malhas 1, 2 e 3.
Passo 1
Identificando as malhas:
Atribuir sentido às correntes de malha:
Se você analisar o circuito, vai perceber que entre as malhas 2 e 3 existe uma supermalha:
Passo 2
Depois de analisar o circuito, vamos equacioná-lo, utilizando a LTK e levando em consideração a supermalha:
Simplificando:
Se você perceber, há duas equações e 3 incógnitas. Por isso precisamos aplicar a LCK no nó da supermalha. Fica tranquilo, vamos ver isso no passo seguinte :)
Passo 3
Analisando o nó da supermalha e aplicando LCK:
Com esta equação, podemos resolver o sistema agora:
Passo 4
Substituindo a equação em e :
Resolvendo o sistema:
Somando as duas equações, fica somente:
Passo 5
Se analisarmos o circuito novamente, veremos que:
Substituindo o valor de na equação :
De acordo com a equação :
Passo 6
Finalmente,
Resposta
Exercício Resolvido #9
Livro Sadiku, p.106, Exercício 3.52
Use a análise de malhas para determinar , e no circuito da figura abaixo:
Passo 1
Vamos lá! A malha 2 e a malha 3, onde se encontram as correntes e , é considerada uma SUPERMALHA.
Portanto as equações segundo LTK são:
Passo 2
Aplicando a lei de Ohm no resistor de :
Substituindo no sistema e simplificando:
Passo 3
Até o momento, temos duas equações e três incógnitas. Precisamos encontrar mais uma equação que relacione as correntes de malha. Para isso, vamos escolher o nó onde aplicaremos a LCK:
Aplicando a LCK no nó :
Pronto, agora temos três equações e três incógnitas:
Passo 4
Agora, vamos resolver esse sistema aí de cima! Isolando na terceira equação:
Substituindo a relação acima na primeira e na segunda equação:
Simplificando:
Somando as duas equações:
Logo:
Finalmente:
Resposta
Exercício Resolvido #10
Livro Sadiku, p.105, Exercício 3.38
Aplique análise de malhas ao circuito da figura abaixo e obtenha
Passo 1
Neste exercício é pedido para calcular . Se analisarmos os sentidos das correntes de malha arbitrados acima, veremos que:
Aplicando a LTK ao circuito, obteremos as seguintes equações:
Aquela fonte de corrente fez um favorzão pra gente e já determinou o !
Reorganizando as equações e substituindo :
Passo 2
Reorganizando as equações e substituindo :
Substituindo também:
Agora é só resolver esse sistema tranquilinho.
Passo 3
Isolando na equação :
Substituindo em
Passo 4
Substituindo os valores encontrados para e na equação de :