Introdução aos Circuitos Magnéticos
Produzido por Alexandre NunesTeoria
Introdução
Está lembrado da lei de Ampère? Então, ela é a lei que rege a produção de um campo magnético através da circulação de corrente por um condutor e é escrita assim:
Onde é a intensidade do campo magnético, medida em ampères-espiras por metro, que é produzido pela corrente .
Para a gente entender melhor o que essa equação quer dizer, vamos a aplicá-la ao exemplo abaixo:
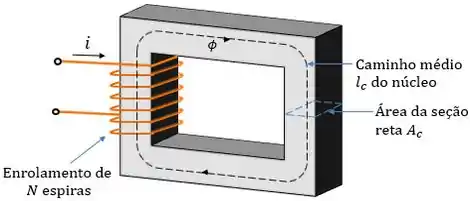
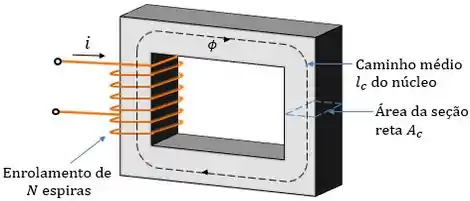
Esse exemplo mostra um núcleo retangular constituído por um material ferromagnético com um enrolamento de espiras de fio enrolados em uma de suas pernas.
Como o núcleo é composto por um material ferromagnético, podemos considerar que todo o campo magnético produzido pela corrente ficará contido no núcleo, de modo que na lei de Ampère o caminho de integração será o comprimento médio no núcleo .
Já a corrente líquida é dada pelo produto do número de espiras com a corrente que circula pelo enrolamento. Podemos escrever a lei de Ampère assim:
Lembrando que estamos escrevendo com subíndice C, porque significa Core de Núcleo, ou seja, tudo que circula pelo núcleo colocamos C.
Então, a intensidade do campo magnético no núcleo, devido à corrente, é:
Em circuitos magnéticos o produto é a força magnetomotriz , ou seja:
Permeabilidade Magnética
A gente relaciona a intensidade de campo magnético e a densidade de fluxo magnético através de uma propriedade do material em que se encontra o campo magnético chamada de permeabilidade magnética .
Para você não se enrolar com esses nomes parecidos, vou fazer um esquema abaixo com o que cada letra representa e suas respectivas unidades no :
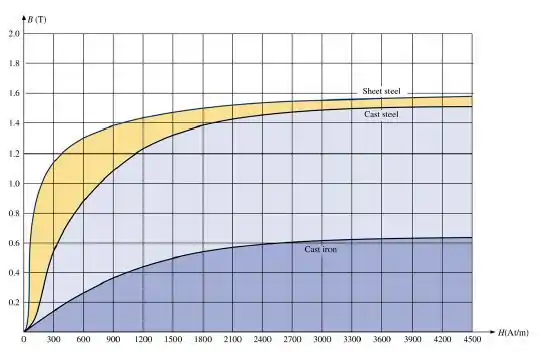
No gráfico acima percebemos que existem diferentes curvas que representam a variação da Densidade de fluxo magnético B com a variação da Intensidade de fluxo magnético H, pois com a mudança do material no qual o fluxo percorre, a permeabilidade magnética varia. Por exemplo, vemos que a variação é maior no tipo de material Chapa de Aço (Sheet Steel) do que no material Ferro fundido (Cast Iron).
Normalmente a permeabilidade dos materiais magnéticos é dada em termos de , que é o seu valor relativo ao valor da permeabilidade do vácuo , ou seja:
Onde a permeabilidade do vácuo é:
Nas máquinas rotativas e transformadores atuais, varia de a Como a permeabilidade magnética é maior que a do ar, o fluxo “prefere” passar pelo núcleo e tem pouca dispersão pelo ar.
Fluxo Magnético
O fluxo magnético que atravessa uma superfície é definido assim:
Mas, podemos considerar que toda a densidade de fluxo magnético será a mesma em uma seção reta de um circuito magnético.
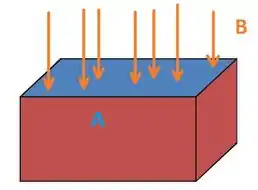
Então, a gente pode jogar essa integral para o espaço e utilizar essa simples equação simples abaixo:
Onde:
Relutância e Permeância
A partir da equação:
No núcleo, podemos escrever a densidade de fluxo magnético assim:
Vimos que a força magnetomotriz pode ser escrita da seguinte forma:
Então, usando a relação entre e :
Substituindo o valor de e escrevendo a em termos do fluxo :
O termo entre parênteses, que multiplica o fluxo na equação, é chamado de relutância do núcleo, ou seja:
Então, temos a seguinte equação que relaciona a força magnetomotriz, o fluxo e a relutância:
Logo, para qualquer circuito magnético, o fluxo pode ser calculado por:
Para entender melhor esses conceitos é só parar para comparar com o que já sabemos. Podemos fazer um paralelo entre a Força Magnetomotriz com a Tensão , as duas são os elementos que forçam a circulação do fluxo magnético no caso de circuitos magnéticos e de corrente no caso de circuitos elétricos. Por outro lado, a relutância se contrapõe a essa circulação de fluxo magnético, assim como a resistência nos circuitos elétricos.
Facilitou, né? Saca essa tabelinha:

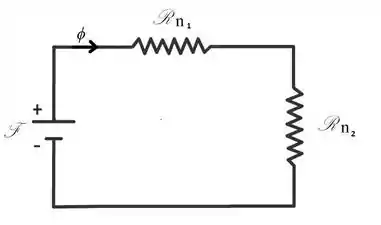
Lembra que o inverso da resistência elétrica era a condutância, no caso do inverso da relutância, também temos um termo que é chamado de permeância :
Agora vamos fazer um exemplo numérico para você ver como funciona essa sopa de letras, partiu?!
Exemplo
Vamos supor que a área da seção reta do núcleo é , o caminho médio é de , ele possui espiras enroladas. A permeabilidade relativa do material do núcleo é e a corrente que circula pelas espiras é igual a 7,45mA. Calcular a relutância do núcleo, o fluxo e o campo magnético.
Passo 1:
O primeiro cuidado que temos que tomar é em relação às unidades. Temos que passar tudo o que está em centímetros para metros.
Além disso, foi dado a permeabilidade relativa . Logo, a permeabilidade do núcleo é
Passo 2:
Podemos encontrar o valor da Intensidade do campo magnético através da igualdade que já conhecemos:
Passo 3:
Como já conhecemos a permeabilidade magnética do núcleo , podemos calcular a Densidade de fluxo magnético :
Substituindo os valores que já sabemos:
Passo 4:
Como estamos considerando que a densidade de fluxo magnético é a mesma por toda a área da seção:
Passo 5:
Em um circuito magnético, a relutância pode ser calculada como a divisão entre a Força magnetomotriz e o fluxo magnético:
E como sabemos, a Força magnetomotriz é igual a:
Logo:
Substituindo os valores já encontrados:
Encontramos:
Pronto!
Agora é fazer os exercícios para fixar a matéria!