Análise de Circuitos Magnéticos
Produzido por Alexandre NunesTeoria
Agora, vamos analisar os circuitos magnéticos como analisamos os circuitos elétricos simples. Esse tipo de análise é a mais comum e simplifica muito a nossa vida, já que as leis de circuitos elétricos já estão em nosso sangue e são válidas nessa análise de circuito magnético.
Vamos começar!
Circuito Elétrico
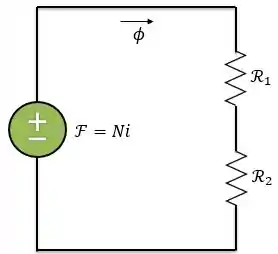
Em um circuito elétrico simples, como o mostrado abaixo, a fonte de tensão injeta ao circuito uma corrente que passa por uma resistência .
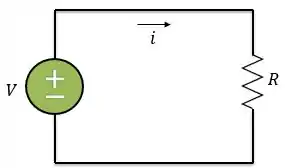
Pela lei de Ohm:
Circuito Magnético
No circuito elétrico o fluxo de corrente é injetado por uma tensão ou uma força eletromotriz. De maneira análoga, em um circuito magnético a força magnetomotriz é a responsável por criar o fluxo .
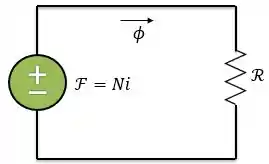
Do mesmo modo que a lei de Ohm, a relação entre a e o fluxo é
Relutância
Como sabemos, podemos calcular a relutância do núcleo pela fórmula abaixo:
As relutâncias em um circuito magnético obedecem às mesmas regras que as resistências em um circuito elétrico. Quando elas estão em série, a relutância equivalente é a soma das relutâncias:
Já quando estão em paralelo:
Exemplo 1 – Circuito Magnético Série
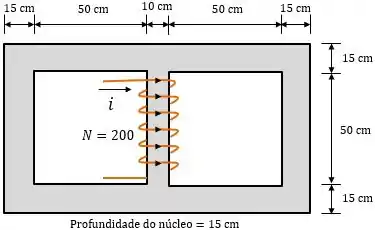
Para você ver como essa análise de circuitos magnéticos facilita muito a nossa vida, vamos fazer o exemplo abaixo. Nele, temos um núcleo ferromagnético, três de seus lados têm a mesma largura e a largura do quarto lado é menor. A profundidade do núcleo é e as outras dimensões são mostradas na figura. Vamos assumir que a e calcular o fluxo que será produzido por uma corrente de ampères.
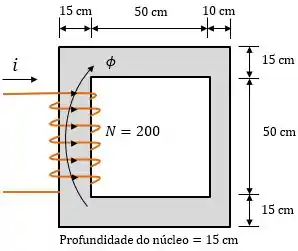
Passo 1
O primeiro passo é calcular as relutâncias. Nesse exemplo temos duas: uma referente aos três lados de mesma largura e a outra referente ao lado de menor largura.
Primeiro vamos determinar os comprimentos médios e .
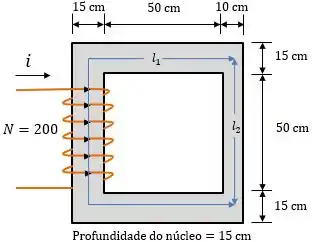
Analisando a figura temos:
Passo 2
Agora, vamos calcular as áreas das seções retas:
Além disso, foi dado a permeabilidade relativa .Logo, a permeabilidade do núcleo é:
Passo 3
Então, substituindo os valores que calculamos, temos as seguintes relutâncias:
Passo 4
Agora que calculamos as relutâncias, vamos desenhar o circuito magnético referente a esse exercício. Como o fluxo é o mesmo para todos os lados do núcleo ferromagnético, o circuito é série e, consequentemente, as relutâncias estão associadas em série.
Portanto, a relutância total do núcleo é:
Passo 5
Podemos calcular a total multiplicando o número de espiras do enrolamento pela corrente que circula por ele.
Passo 6
Pela analogia de circuitos elétricos com circuitos magnéticos temos:
Logo, o fluxo é calculado por:
Pronto! Agora vamos ver um caso em que as relutâncias estão associadas em paralelo.
Exemplo 2 – Circuito Magnético Paralelo
Agora, temos o núcleo abaixo com a mesma permeabilidade relativa . As dimensões estão mostradas na figura. Se na bobina houver espiras enroladas em torno da perna central do núcleo e se a corrente na bobina for , quais serão os valores de fluxo para as pernas esquerda, central e direita do núcleo?
Passo 1
Nesse exemplo temos três relutâncias: uma referente à perna central, uma referente ao lado esquerdo e outra referente ao lado direito, que são respectivamente:
Primeiro vamos determinar os comprimentos médios e as áreas das seções retas:
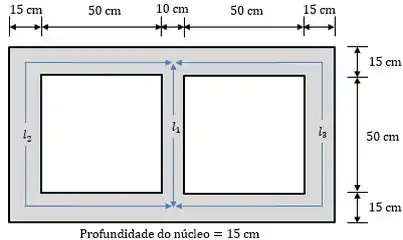
Analisando a figura temos:
Agora, vamos calcular as áreas das seções retas:
Como o núcleo tem a mesma permeabilidade relativa do que o exemplo anterior:
Passo 2
Então, substituindo os valores que calculamos, temos as seguintes relutâncias:
Passo 3
Agora que calculamos as relutâncias, vamos desenhar o circuito magnético referente a esse exemplo.
Nesse caso, o fluxo produzido na perna central se dividirá em dois: um seguindo para a esquerda e outro para a direita. Logo, o circuito é paralelo e, consequentemente, as relutâncias estão associadas em paralelo.
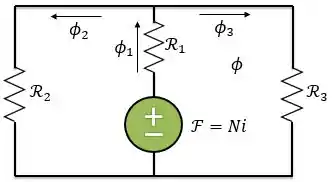
Como o fluxo é o análogo à corrente em um circuito elétrico, temos:
Além disso, a relutância total do núcleo é:
Passo 4
Podemos calcular a total multiplicando o número de espiras do enrolamento pela corrente que circula por ele:
Passo 5
Pela analogia de circuitos elétricos com circuitos magnéticos temos:
Logo, o fluxo é calculado por:
Passo 6
Agora, vamos calcular os fluxos da esquerda e da direita utilizando o mesmo princípio de divisor de corrente em circuitos elétricos.
Como podemos ver, o fluxo gerado na perna central se divide igualmente entre os dois caminhos, o que era de se esperar, já que a relutância da região da direita é igual à da esquerda. Isso prova mais uma vez a analogia entre os circuitos magnéticos e elétricos.
Quando tínhamos um circuito elétrico com dois resistores iguais ligados em paralelo, a corrente se dividia igualmente. Metade passava por um resistor e a outra metade no outro.
Agora é praticar bastante!