Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Divisor de Corrente

Ver Todos os Exercícios

Teoria

Fala aí! Seja bem vindo ao Responde Aí! Bora conversar sobre Divisor de Corrente e Tensão?!

Pra que Serve um Divisor de Corrente?

Imagina que você quer ligar uma lâmpada que consome, em condições normais, uma corrente de mas a sua fonte tem uma corrente limite de . A lâmpada vai queimar, certo?!

É ai que entra o divisor de corrente! Conseguimos dividir um corrente criando um circuito paralelo, nesse caso a corrente tem mais de um caminho para percorrer, logo ela se divide! Se liga na imagem abaixo:

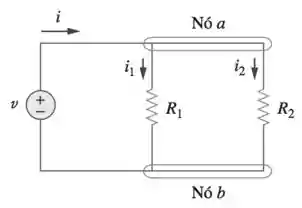
Resistores em paralelo
Resistores em paralelo

Quando temos um circuito como o mostrado acima, percebemos que a tensão entre os nós e é igual a tensão da fonte , já a corrente vai se dividir de uma forma inversamente proporcional às resistências!

📢 Clique para ver mais:

Como calcular um divisor de corrente?

Ou então continua comigo no textinho!

Quando dividimos a corrente, temos a mesma tensão aplicada aos resistores e . Relembrando a Primeira lei de Ohm:

Assim teremos duas correntes proporcionais aos valores de cada resistor:

Vimos que o circuito pode ser simplificado por uma resistência equivalente ():

e sabendo que:

Substituindo uma na outra, temos que:

Com isso podemos perceber que a maior corrente fluirá pelo menor resistor!

Divisores de tensão

Cada resistor “consome” uma tensão entre seus terminais, isso quer dizer que se tivermos dois resistores em série, entre eles haverá um que causará uma queda de tensão menor e outro uma maior, que são proporcionais aos valores dos resistores. Difícil? Vou explicar melhor, saca só.

As quedas de tensão e nos resistores e são menores que (tensão da fonte).

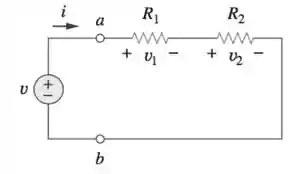
Circuito com dois resistores
Circuito com dois resistores

Como calcular um divisor de tensão?

Começamos usando a Lei de Ohm:

Pela Lei de Kichorff:

Isolando a corrente :

Aplicando isso nas fórmulas de e temos:

A ligação série é muito útil para converter tensões maiores, para menores quando tem dois resistores ligados em uma só fonte!

Circuito aberto e Curto-circuito

Caso um dos resistores for zero como no caso abaixo, a corrente passará toda por esse ramo, pois ele oferece menor resistência a passagem dela. Chamamos isso de curto-circuito.

⁍
⁍

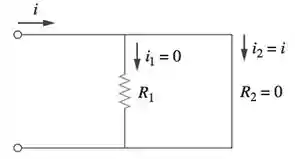
Caso um dos ramos esteja em aberto como na figura abaixo:

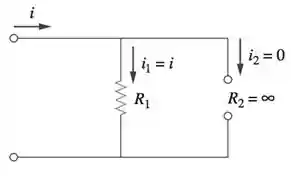
A abertura em
A abertura em

Não existe corrente que circule por um “caminho aberto”, isso é o mesmo que uma resistência tão alta que a corrente não flui por ela. Assim, quando temos um Circuito aberto, dizemos que a resistência é infinita!

Agora vamos praticar com exercícios 👇

Divisores de tensão

Circuito aberto e Curto-circuito

Exercícios Resolvidos

Exercício Resolvido #1

Boylestad – 12 ed. – Capítulo 6 - Exercício 31 - Adaptada

  1. Determine uma das correntes desconhecidas da figura usando a regra de divisor de corrente.
  2. Determine a outra corrente usando a Lei de Kirchhoff de corrente.

Passo 1

Pela regra do divisor de corrente, vamos calcular I 1 :

I 1 = 20 m A * ( 8 k 8 k + 2 k )

I 1 = 20 m A * 0,8 = 16 m A

Passo 2

Segundo a Lei de Kirchhoff para correntes, a soma das correntes que entram em um nó é igual a soma das correntes que saem desse nó, logo:

I 1 +   I 2 = 20 m A

16 m A +   I 2 = 20 m A

  I 2 = 20 m A - 16 m A = 4 m A

Resposta

I 1 = 16 m A

I 2 = 4 m A

Exercício Resolvido #2

Descubra os valores desconhecidos para o circuito usando as informações fornecidas:

Passo 1

Por todos os resistores estarem em paralelo, eles tem a mesma queda de tensão, porém corrente diferentes.

Passo 2

Assim, podemos calcular o paralelo entre os resistores por onde passam as correntes I 2 e I 3 :

R 23 =   4 k * 4 k 4 k + 4 k

R 23 =   2 k Ω

Passo 3

Logo a corrente I 1 é resultado de um divisor de corrente entre 1 k Ω e R 23 :

I 1 =   100 m A *   R 23 R 23 + 1 k Ω

I 1 =   100 m A *   2 k Ω 2 k Ω + 1 k Ω

I 1 = 66,66 m A

Passo 4

Próximo passo para descobrir a corrente I 2 , devemos fazer o paralelo entre os resistores por onde passam as correntes I 1 e I 3 : R 1 3 =   1 k * 4 k 1 k + 4 k

R 13 = 0,8 k Ω  

Passo 5

Logo a corrente I 2 é resultado de um divisor de corrente entre 4 k Ω e R 1 3 :

I 2 =   100 m A *   R 1 3 R 1 3 + 4 k Ω

I 2 =   100 m A *   0,8 k Ω 0,8 k Ω + 4 k Ω

I 2 = 16,67 m A

Passo 6

Como os resistores por onde passam as correntes I 2 e I 3 são iguais e estão em paralelo, as correntes I 2 e I 3 são iguais:

I 2 =   I 3

I 2 =   I 3 = 16,67 m A

I 3 = 16,67 m A

Resposta

I 1 = 66,66 m A

I 2 = 16,67 m A

I 3 = 16,67 m A

Exercício Resolvido #3

Boylestad – 12 ed. – Capítulo 6 - Exercício 30

Com base somente nos valores dos resistores, determine todas as correntes para a configuração do circuito. Não use a Lei de Ohm.

Passo 1

Vamos descobrir a corrente I T através da correte que circula no resistor de 6Ω. Para isso vamos substituir as demais resistências por uma resistência equivalente.

Como todos os resistores estão em paralelo:

  • 12Ω em paralelo com 18Ω:

    • 12 * 18 12 + 18

    216 30 = 7,2 Ω

  • 2Ω em paralelo com 7,2Ω:

    • 2 * 7,2 7,2 + 2

    14,4 9,2 = 1,57 Ω

    Assim pela regra do divisor de corrente:

    I 1 =   ( I T * 1,57 ) / ( 1,57 + 6 )

    9 =   ( I T * 1,57 ) / 7,57

    I T = 43,4 A

    Passo 2

    Calculando a corrente que passa pelo resistor 2Ω, devemos inicialmente fazer o paralelo entre todos os demais resistores:

  • 12Ω em paralelo com 18Ω:

    • 12 * 18 12 + 18

    216 30 = 7,2 Ω

  • 6Ω em paralelo com 7,2Ω:

    • 6 * 7,2 7,2 + 6

    4 3,2 13,2 = 3,27 Ω

    A corrente que circula no resistor de 2Ω:

    I 3 =   ( I T * 3,27 ) / ( 3,27 + 2 )

    I 3 = ( 43,4 * 3,27 ) / ( 3,27 + 2 )

    I 3 =   26,9 A

    Passo 3

    Calculando a corrente que passa pelo resistor 12Ω, devemos inicialmente fazer o paralelo entre todos os demais resistores:

  • 6Ω em paralelo com 18Ω:

    • 6 * 18 6 + 18

    108 24 = 4,5 Ω

  • 2Ω em paralelo com 4,5Ω:

    • 2 * 4,5 2 + 4,5

    9 6,5 = 1,38 Ω

    A corrente que circula no resistor de 12Ω:

    I 2 =   ( I T * 1,38 ) / ( 1,38 + 1 2 )

    I 2 = ( 43,4 * 1,38 ) / ( 1,38 + 1 2 )

    I 2 =   4,48 A

    Passo 4

    Calculando a corrente que passa pelo resistor 18Ω, devemos inicialmente fazer o paralelo entre todos os demais resistores:

  • 6Ω em paralelo com 12Ω:

    • 6 * 1 2 6 + 1 2

    72 18 = 4 Ω

  • 2Ω em paralelo com 4Ω:

2 * 4 2 + 4

8 6 = 1,3 3 Ω

A corrente que circula no resistor de 18Ω:

I 4 =   ( I T * 1,3 3 ) / ( 1,3 3 + 1 8 )

I 4 = ( 43,4 * 1,3 3 ) / ( 1,3 3 + 1 8 )

I 4 =   2,99 A

Resposta

I T = 43,4 A

I 2 =   4,48 A

I 3 =   26,9 A

I 4 =   2,99 A

Exercício Resolvido #4

Boylestad – 12 ed. – Capítulo 5 - Exercício 27

Usando a regra do divisor de tensão, descubra a tensão indicada na figura:

Passo 1

O primeiro passo é perceber que como a tensão desejada é a mesma que a soma das quedas de tensão em cima dos resistores de 1,5Ω, 0,6Ω e 0,9Ω, podemos substituir esses resistores por uma resistência equivalente:

R e q = 1,5 + 0,6 + 0,9 = 3,0 Ω

Passo 2

Agora podemos calcular o divisor de tensão com os demais resistores, lembrando que a queda de tensão em cima de um resistor é proporcional ao valor desse resistor. Assim:

V 3 = E   R 3 R e q + R 3

V = 0,72   3 2,5 + 0,5 + 3

V = 0,72 2 = 0,36 V

Resposta

V = 0,36 V

Exercício Resolvido #5

No circuito da figura, o contato divide a resistência do potenciômetro entre α R e 1 - α R , 0 ≤ α ≤ 1 . Determine v o / v S .

Passo 1

Perceba que o contato é um curto circuito feito em uma parte do resistor, portanto, o circuito irá “perder” α R de resistência, e então o circuito ficará assim:

Passo 2

Usando divisor de tensão, temos que:

v 0 = v s   . 1 - α R 1 - α R + R

E então:

v 0 v s = 1 - α R 1 - α R + R

v 0 v s = 1 - α R 2 - α R

∴

v 0 v s = 1 - α 2 - α

Resposta

v 0 v s = 1 - α 2 - α

Exercício Resolvido #6

A resistência equivalente de dois resistores R 1 e R 2 em paralelo é 10 / 3 ohms. A corrente que penetra no circuito paralelo divide-se entre dois na proporção de 1 para 1 . Determine R 1 e R 2 .

Passo 1

Vamos desenhar a situação:

O enunciado nos diz que as correntes se dividem igualmente, então:

I 1 = I 2 = I R 1 R 1 + R 2 = I R 2 R 1 + R 2

Portanto:

R 1 = R 2

Passo 2

Tá faltando uma informação, certo?

Vamos usar que a resistência equivalente é 10 / 3 :

R 1   .   R 2 R 1 + R 2 = 10 3

Usando que elas são iguais:

R 1 2 2 R 1 = R 1 2 = 10 3

R 1 = R 2 = 20 3

Resposta

R 1 = R 2 = 20 3   Ω

Exercício Resolvido #7

Sendo de 14 ampères a corrente no resistor de 5 ohms da figura, determinar a tensão constante V .

Passo 1

Antes de usar divisor de corrente, vamos fazer a associação em paralelo dos dois resistores de 10 Ω :

R e q 1 = 10 2 = 5 Ω

Se chamarmos de I a corrente que sai da fonte, podemos agora usar o divisor:

i = I   . 5 5 + 5 = I 2

Como o enunciado nos diz que i = 14   A :

I = 28   A

Passo 2

Agora, para usarmos a 1ª lei de Ohm, precisamos da resistência geral do circuito. Para isso falta mais uma associação em paralelo e uma em série:

R e q = 5   .   5 5 + 5 + 2 = 4,5 Ω

E então:

V = R e q I

V = 4,5   .   28 = 126   V

Resposta

126 volts.

Exercício Resolvido #8

Determine i 1 a i 4 no circuito da figura.

Passo 1

Primeira coisa a se fazer é redesenhar o circuito para entender melhor:

Com isso podemos eles estão TODOS, em paralelo.

Passo 2

Para encontrar a corrente i 1 que passa pelo resistor de 50 Ω , devemos descobrir a resistência equivalente que está em paralelo com esse resistor e a fonte de corrente. Faremos a resistência equivalente entre os resistores:

1 R e q 1 = 1 60 + 1 40 + 1 200

R e q 1 = 21,43 Ω

Passo 3

Agora vamos perceber que a corrente da fonte I 1 de 16A aponta para baixo, logo está no sentido oposto do que deveria para a corrente i 1 ser positiva (marcado em vermelho). Vamos indicar isso como uma corrente total negativa na nossa fórmula.

Passo 4

Logo para calcular a corrente i 1 faremos a aplicação da fórmula de divisor de corrente.

i 1 =   i R e q 1 R e q 1 +   R 1

Substituindo os valores:

i 1 =   - 16 21,43 21,43 +   50

i 1 =   - 4,8 A

Passo 5

Para encontrar a corrente i 4 faremos o mesmo procedimento anterior, porém com os outros resistores que estão em paralelo com o resistor de 60 Ω :

1 R e q 2 = 1 40 + 1 50 + 1 200

R e q 2 = 20 Ω

Passo 6

Vamos considerar a corrente total negativa como já falamos anteriormente e aplicar os valores na fórmula do divisor de corrente:

i 4 =   i R e q 2 R e q 2 +   R 4

Substituindo os valores:

i 4 =   - 16 20 20 +   60

i 4 =   - 4 A

Tranquilão, né?

:D

Resposta

i 1 = - 4,8 A

i 4 = - 4 A

Exercício Resolvido #9

Obtenha v e i no circuito da figura.

Passo 1

A primeira coisa a perceber aqui é que estamos trabalhando com condutância, se liga na unidade dos resistores, é Siemens!

Portanto, quando formos fazer as associações, devemos usar o valor inverso ao que está na imagem, beleza?

Vamos começar então fazendo a associação em série dos resistores de 6   S e 3   S :

R e q 1 = 1 6 + 1 3 = 1 2   Ω

Passo 2

Agora vamos fazer uma associação em paralelo:

R e q 2 = 1 2   . 1 2 1 2 + 1 2 = 1 4   Ω

Passo 3

E nós vamos repetir o passo da associação em série.

R e q 3 = 1 4 + 1 4

Passo 4

E o circuito fica assim:

Vamos usar divisor de corrente para descobrir o valor de i :

i = 9   . 1 1 + 0,5 = 6   A

Passo 5

E portanto, temos que:

i 0 = 9 - 6 = 3   A

Podemos usar então a 1ª lei de Ohm para encontrar v :

v = 1   .   3 = 3   V

Resposta

i = 6   A

v = 3   V

Exercício Resolvido #10

Para o circuito da figura, determine i 1 a i 5 .

Passo 1

Vamos começar encontrando i 1 , para isso, vamos ter que fazer o cálculo da resistência equivalente, e vai ajudar se nós “guardarmos” os estágios desse cálculo, beleza?

Primeiro estágio: Paralelo entre os resistores de 1 Ω e 2 Ω :

R e q 1 = 1   .   2 1 + 2 = 2 3 = 0.667 Ω

Passo 2

Segundo estágio: Paralelo entre 4 Ω e 2 3   Ω :

R e q 2 = 4   . 2 3 4 + 2 3 = 8 14 = 0.571   Ω

Passo 3

Terceiro estágio: série entre os restantes.

R e q 3 = 3 + 0.571 = 3.571   Ω

E usando a 1ª lei de Ohm:

i 1 = 2 00 3.571 = 56 A

Passo 4

No primeiro estágio, podemos encontrar a corrente que passa pelo resistor de 4   Ω , que é a corrente i 2 :

i 2 = i 1 2 3 4 + 2 3 = i 1 2 14 = i 1 7

Portanto:

i 2 = 8   A

E então, podemos usar que:

i 3 = 56 - 8 = 48   A

Passo 5

E usando divisor de corrente, achamos i 4 e i 5 :

i 5 = i 3 1 1 + 2 = i 3 3

i 5 = 48 3 = 16 A

E então:

i 4 = 48 - 16 = 32   A

Resposta

i 1 = 56   A

i 2 = 8   A

i 3 = 48   A

i 4 = 32   A

i 5 = 16   A

Exercícios de Livros Relacionados

Conecte uma fonte de tensão de 6V entre os terminais a-b na Figura P3.9 (b), com o terminal positivo na parte superior.a) Use a divisão de tensão para determinar a tensão nos terminais do resistor de
O amperímetro descrito no Problema 3.39 é usado para medir a corrente i o no circuito da Figura P3.38. Qual é o erro percentual no valor medido?
4 O fundo de escala do voltímetro mostrado na Figura P3.44(a) é 500 V. O medidor está calibrado para 100 mV e 0,5 mA. Qual é o erro percentual na leitura do medidor se ele for usado para medir a tensã
Projete um voltímetro de d’Arsonval que terá as três faixas de tensão mostradas na Figura P3.48. a) Especifique os valores de R1, R2 e R3. b) Suponha que um resistor de 750 kV esteja ligado entre o te
Calcule todas as tensões de saída possíveis, inferiores a 14 V, que podem ser obtidas pela construção de divisores de tensão com uma fonte de 14 V em série com três resistores cujos valores são, respe