Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Potência

Ver Todos os Exercícios

Teoria

Fala pessoal, tudo certinho?

Agora vamos falar sobre a potência em elementos passivos, no caso, os resistores.

Conceito de Potência

Recordando rapidinho o conceito de potência:

“Potencia é uma variação da energia em uma determinada variação do tempo. “

Mas como assim?

Simples, potência ( p ) é a velocidade com que, se consome ou se absorve, uma energia medida em watts (W).

p = d w d t  

Onde w é a energia em Joules, t é o tempo medido em segundos, e p é a potência medida em watts (W).

Potencia elétrica

Agora que sabemos o conceito de potência, vamos associar com a eletricidade.

Se potencia é a velocidade que consome uma energia em um determinado tempo, essa energia pode ser o que?

A corrente elétrica, isso mesmo! E corrente elétrica, é uma quantidade de carga que flui em um determinado tempo pelo circuito.

i = d q d t

Onde q é a carga em Coulomb e t é o tempo em segundos.

Outro detalhe devemos nos atentar, é que, Joule é equivalente a Coulomb x Volts

J = C * [ V ]

Logo temos que, resolvendo a equação e fazendo uma análise dimensional:

p = d w d q * d q d t = V * C C * A = V * [ A ] = V i

Farei algumas relações para tornar nossa vida mais fácil em alguns exercícios.

Lembra que eu disse que

V = R i

Pois é, vamos reformular mais duas equações de potência. Isolando o i temos que

i = V R

portando ficamos assim, substituindo v

p = R i i = R i 2

e substituindo i

p = v v R = v 2 R

Tá ai, mais duas fórmulas para resolver os exercícios facilmente.

Okay, definindo então que potência é igual a tensão vezes a corrente, a potência pode ser negativa ou positiva. Por que? Porque ela pode ser consumida ou fornecida por algo.

Potência consumida x Potência fornecida

Ó é simples. Pelo sinal da corrente, podemos dar o mesmo sinal para a potência, pois assim, o sinal determina se a corrente está entrando ou saindo. Ou seja, fornecendo ou consumindo.

Potência é consumida por elementos em que a corrente entra pelo polo positivo:

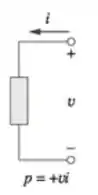
Um exemplo de potência consumida é por resistores. Percebemos que a convenção de sinal é positiva para potência consumida.

Vamos ver um exemplo:

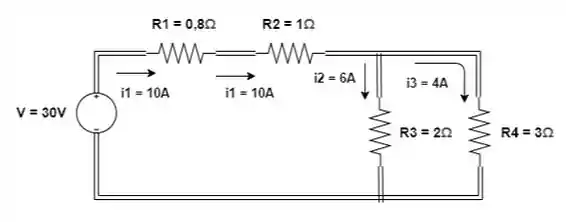
Nesse circuito vemos vários resistores nos quais circulam correntes. Agora vamos marcar as quedas de tensão nos resistores, tanto seus polos quanto seu valor:

v 1 =   i 1 *   R 1 = 10 * 0,8 = 8 V

v 2 =   i 2 *   R 2 = 10 * 1 = 10 V

v 3 =   i 2 *   R 3 = 6 * 2 = 12 V

v 4 =   i 3 *   R 4 = 4 * 3 = 12 V

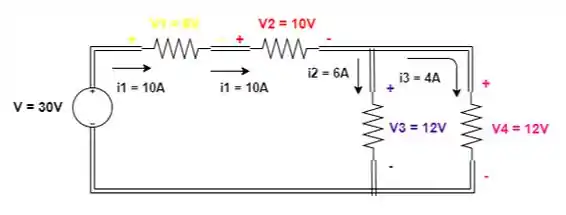
Como as correntes estão entrando nos polos positivos das quedas de tensão, a potência é consumida e o sinal convencional é positivo:

p 1   =   i 1 *   v 1 = 10 * 8 = + 80 W

p 2   =   i 1 *   v 2 = 10 * 10 = + 100 W

p 3   =   i 2 *   v 3 = 6 * 12 = + 72 W

p 4 =   i 3 *   v 4 = 4 * 12 = + 48 W

A potência é fornecida por elementos onde a corrente sai pelo polo positivo, como as fontes de tensão:

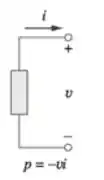
Percebemos que a convenção de sinal é negativa para potência fornecida.

Vamos continuar o exemplo anterior, olhando para a fonte de tensão:

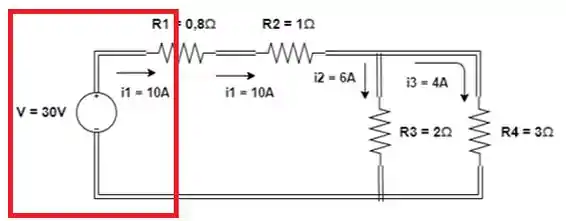
A corrente sai pelo polo positivo da fonte de tensão, logo sua potência é:

p f o n t e =   -   v f o n t e * i f o n t e =   - V *   i 1 =   - 30 * 10 =   - 300 W

Último detalhe para esse assunto é que em um circuito, a soma de todas as potências de cada elemento, deve ser igual a zero. Isso é o princípio de conservação de energia. Ou seja galerinha, tudo que é fornecido, o circuito consumiu, nada a mais e nada a menos.

∑ p = 0

Vamos ver isso no nosso exemplo?

∑ p = p f o n t e + p 1 + p 2 + p 3 + p 4 =   - 300 + 80 + 100 + 72 + 48 = 0

Bom é isso aí e vamos arrasar na prova!

Energia Elétrica

Depois de ver o conceito de potência elétrica, vamos entender um pouquinho por último sobre como funciona um consumo de energia elétrica no nosso dia a dia.

Vocês sabem me dizer o que consome energia elétrica em casa???

TUDO! Não tudo, mas tudo que está conectado na tomada da sua casa, ou que utiliza da energia elétrica para funcionar, como lâmpadas, cerca elétrica, entre outros.

Como a companhia de energia elétrica da sua cidade mede o seu consumo em casa?

Conta de Luz

Se alguém já teve a curiosidade de dar aquela olhadinha de como funciona uma conta de luz da sua casa, sabe que a companhia muda a o jeito de mostra o consumo de energia na sua casa, utilizando de técnicas como:

  • Mostrar em kW, ou seja, dividir por 1000
  • Mostrar em função de hora (kWh)

Vou lhes ensinar a fazer esse cálculo.

Vamos supor que você tenha um aparelho em casa que consuma 100 W. Se esse aparelho ficar ligado dia e noite, sem desligar. Quanto no fim do mês, esse consumo representará em sua conta de luz?

Bom, é simples, supondo o mês ter 30 dias, e o dia ter 24 horas, temos que:

t e m p o = 30 * 24 = 720   h o r a s

E a potência desse aparelho em kW é:

p o t ê n c i a = 100   W 1000 = 0,1   k W

Com isso temos a consumo que será

e n e r g i a   c o n s u m i d a =   p o t ê n c i a * t e m p o = 0,1 * 720 = 72 k W h

Caso você queira saber o quanto isso representa em R$ (Reais), na sua conta, basta multiplicar esse valor do consumo pelo valor do kWh da sua cidade (que está informado na conta de energia).

Viu? Facinho! Agora fazer exercício, e ficar atento para as contas de energia!

Potência consumida x Potência fornecida

Energia Elétrica

Conta de Luz

Exercícios Resolvidos

Exercício Resolvido #1

Três resistores R 1 , R 2 e R 3 estão em série com uma tensão constante V . A tensão em R 1 é 20 volts, a potência em R 2 é 25 watts e R 3 é de 2 ohms. Calcular a tensão V , sendo a corrente 5 ampéres.

Passo 1

Sabemos que, como os resistores estão em série, podemos somar as tensões nos resistores para encontrar a tensão V , certo?

No primeiro resistor, já nos foi dado a tensão nele, que é de 20   V , portanto:

V 1 = 20   V

Passo 2

Já no segundo resistor, temos a potência consumida, e também temos a corrente que passa por ele. Usando a expressão da potência:

P = U I

25 = V 2   .   5

V 2 = 5   V

Passo 3

No terceiro resistor, nos foi dado a resistência, e como a corrente que passa por resistores em série é a mesma, podemos usar a 1ª lei de Ohm:

U = R I

V 3 = 2   .   5

V 3 = 10   V

Passo 4

Finalmente, nos falta encontrar V :

V = V 1 + V 2 + V 3 = 20 + 5 + 10 = 35   V

Resposta

35   V

Exercício Resolvido #2

UFF- Lista de Exercícios sobre Circuitos Elétricos

Uma lâmpada de 100   W é ligada em uma tomada-padrão de 120   V .

  1. Qual o custo mensal para deixar a luz acesa continuamente? Suponha que a energia elétrica custe, com impostos, R $   0,60 / kW⋅h ;
  2. Qual a resistência da lâmpada?
  3. Qual a corrente na lâmpada?
  4. A resistência é diferente quando a lâmpada é desligada?

Passo 1

  1. Qual o custo mensal para deixar a luz acesa continuamente? Suponha que a energia elétrica custe, com impostos, R $   0,60 / kW⋅h ;

    2. Sabendo que a potência dissipada pela lâmpada é de 100   W , ou 0,1   kW e supondo o mês com 30   dias , o custo é dado por:

    Total=Potência × Tempo × Custo

    Total = 0,1 × 30 × 24 × 0,6

    Total = R $   43,20

    Passo 2

  2. Qual a resistência da lâmpada?

    3. Como já temos a potência P e a voltagem V , para calcular a resistência R , basta usar a relação:

    P = V 2 R

    R = V 2 P

    Onde:

    P = 100   W ;

    V = 120   V ;

    Logo:

    R = 120 2 100

    R = 144   Ω

    Passo 3

  3. Qual a corrente na lâmpada?

    4. Agora que temos a resistência R e a voltagem V , basta usar a Lei de Ohm:

    V = R I

    I = V R

    Onde:

    V = 120   V ;

    R = 144   Ω ;

    Logo:

    I = 120 144

    I = 0,83   A

    Passo 4

  4. A resistência é diferente quando a lâmpada é desligada?

Não, porque a resistência é uma característica da lâmpada, que independe se a mesma está acesa ou apagada.

Resposta

a. R $   43,20 ;

b. R = 144   Ω ;

c. I = 0,83   A ;

d.Não, porque a resistência é uma característica da lâmpada.

Exercício Resolvido #3

David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3 , 8º ed. Rio de Janeiro: LTC , 2006, pp 163-44.

Na primeira figura abaixo um resistor de 20 Ω é ligado a uma bateria. A segunda figura mostra a energia térmica E t gerada pelo resistor em função do tempo t . A escala vertical é definida por E s = 2,5 m J e a escala horizontal é definida por t s = 4,00 s . Qual a diferença de potencial entre os terminais da bateria?

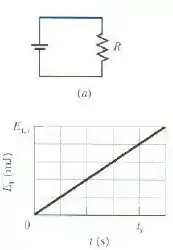
Passo 1

Daí eu te pergunto: Qual o papel de um resistor?

Justamente transformar a energia elétrica em energia térmica, certo?

Esse gráfico aí vai nos mostrar o quanto que ele vai transformar essa energia em função do tempo.

Mas lembra aí, existe alguma parada que relaciona energia com tempo?

Yes! A potência, que pode ser calculada nada mais nada menos por:

P = E Δ t

Nesse caso, teremos que:

Como em t s temos 4 quadradinhos e isso vale 4 s , cada quadradinho na escala horizontal terá 1 s . Logo, poremos fazer:

P = E Δ t = 2,5 m J 5 s = 5 . 10 - 4 W

Passo 2

Show! Já temos a potência. Agora devemos relacioná-la com a resistência e com a voltagem, pois são os dados que temos e o que queremos achar.

Sabe de alguma coisa formula que relaciona os três? Eu sei!

P = V 2 R

Isolando o V , teremos:

V = R . P = 20.5 . 10 - 4 = 0,1 V

Resposta

V = 0,1 V

Exercício Resolvido #4

Um resistor de 10 ohms está em série com uma associação paralela de dois resistores de 15 e 5 ohms. Sendo 6 ampères a corrente constante no resistor de 5 ohms, qual a potência total nos três resistores?

Passo 1

Temos a resistência e a corrente em um resistor, nos falta descobrir a corrente que passa pelos outros dois, certo?

O resistor de 15   Ω está em paralelo com o de 5   Ω , para descobrirmos a corrente que passa pelo resistor de 15   Ω , precisamos lembrar que a corrente é inversamente proporcional à resistência, e então:

I 15 = I 5 3 = 6 3 = 2   A

Passo 2

E para descobrir a corrente que passa pelo resistor de 10   Ω , basta usarmos a lei de Kirchoff das correntes:

I 10 = I 5 + I 15 = 2 + 6 = 8   A

Passo 3

Para encontrar a potência total, nos basta somar a potência de cada um, lembrando que:

P = R I 2

Temos:

P t o t a l = 10   .   8 2 + 5   .   6 2 + 15   .   2 2

P t o t a l = 640 + 180 + 60

P t o t a l = 880   W

Resposta

880 watts.

Exercício Resolvido #5

A queda de tensão em uma torradeira de 1,5 k W que absorve uma corrente 12 A é:

(a) 18 k V

(b) 125 V

(c) 120 V

(d) 10,42 V

Passo 1

Aqui nós vamos usar a seguinte expressão:

P = U I

Substituindo os valores:

1500 = U   .   12

Portanto:

U = 125   V

Resposta

125   V

Exercício Resolvido #6

A corrente máxima que um resistor de 80 k Ω / 2 W pode conduzir com segurança é:

(a) 160 k A

(b) 40 k A

(c) 5 m A

(d) 25 μ A

Passo 1

Quando o problema nos diz sobre “conduzir com segurança”, temos que associar à potência que esse resistor suporta. E então usamos a seguinte expressão:

P = R I 2

2 = 80000   .   I 2

I 2 = 2 80000 = 1 40000

I = 1 200 = 5   .   10 - 3

I = 5   m A

Resposta

5   m A

Exercício Resolvido #7

Determine a resistência quente de uma lâmpada de 60 W / 120 V .

Passo 1

Aqui vamos usar a expressão que usa os dois valores do enunciado, beleza?

P = V 2 R

60 = 120 2 R → R = 240   Ω

Resposta

240   Ω

Exercício Resolvido #8

Sadiku, Matthew N. O.; Alexander, Charles K.; Livro: Fundamentos de Circuitos Elétricos, 5° ed. p.61, Exercício 2.19

A partir da figura, determine I , a potência dissipada pelo resistor e a potência fornecida por cada fonte.

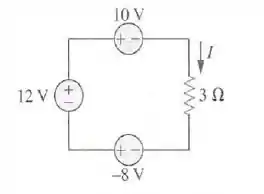
Passo 1

O primeiro passo é identificar a tensão que está sendo aplicada sobre o resistor, beleza?

Para isso, vamos caminhar no circuito do terminal de cima do resistor até o terminal de baixo, passando pelas fontes. Então:

V = - 10 + 12 - 8 = - 6   V

Portanto, de fato a corrente está fluindo no sentido inverso do que está indicado no circuito.

Passo 2

Usando então a 1ª lei de Ohm:

U = R I

- 6 = 3   I

I = - 2   A

Passo 3

A potência dissipada no resistor pode ser calculada como:

P R = R *   I 2

P R = 3 *   ( - 2 ) 2

P R = 12 W

Passo 4

Para então acharmos a potência fornecida por cada fonte, lembrando que o sinal é negativo para as fontes que tiverem fornecendo potência. Mas como sabemos se ela está fornecendo potência ou consumindo? Olhando por onde passa a corrente:

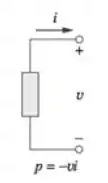
A potência na fonte de 10V tem a corrente saindo de seu polo positivo, logo está fornecendo potência:

P 1 = - V 1   .   I

P 1 = - 10   .   2 = - 20   W

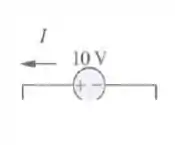
Para a segunda fonte:

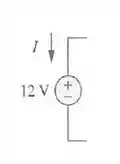
A potência na fonte de 12V tem a corrente entrando de seu polo positivo, logo está consumindo potência:

P 2 = + 12   .   2 = + 24   W

E para a última, podemos inverter a fonte de tensão e seu valor para enxergar melhor:

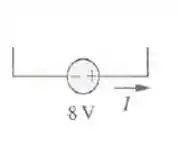
Como a corrente está saindo pelo polo positivo, a potência está sendo fornecida pela fonte:

P 3 =   - 8   .   2 = - 16   W

Resposta

I = - 2   A

P R = 12 W

P 1 = - 20   W ; P 2 = 24   W ; P 3 = - 16   W

Exercício Resolvido #9

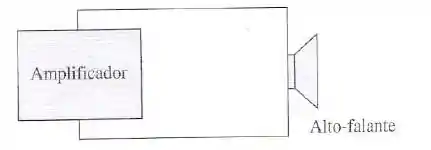
Um alto-falante é conectado a um amplificador, conforme mostrado na figura. Se um resistor de 10 Ω consumir uma potência máxima de 12 W do amplificador, determina a potência máxima que um alto-falante de 4 Ω consumirá.

Passo 1

Para fazermos essa questão, precisamos primeiramente perceber que o amplificador irá sempre fornecer a mesma tensão para o alto-falante, em seguida, devemos lembrar da seguinte expressão da potência:

P = V 2 R

Esta expressão nos mostra que a potência é inversamente proporcional à resistência, portanto:

P 10 P 4 = 4 10 → P 4 = 5 2 P 10

E então:

P 4 = 5 2   12 = 30   W

Resposta

30   W

Exercício Resolvido #10

David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3 , 8º ed. Rio de Janeiro: LTC , 2006, pp 126-39

Um aquecedor por irradiação de 1250   W é fabricado para operar em 115   V .

  1. Qual será a corrente no aquecedor?
  2. Qual a resistência da bobina de aquecimento?
  3. Quanta energia térmica é produzida em 1h pelo aquecedor?

Passo 1

  1. Qual será a corrente no aquecedor?

    2. Aqui não tem muito mistério, o problema nos dá a potência P e a voltagem V . Pra calcular a corrente I , basta usar a relação:

    P = V I

    I = P V

    Onde:

    P = 1250   W ;

    V = 115   V ;

    Logo:

    I = 1250 115

    I = 10,86   A

    Passo 2

  2. Qual a resistência da bobina de aquecimento?

    3. Novamente, já temos a voltagem V e a corrente I , agora, pra calcular a resistência R é só usar a Lei de Ohm:

    V = R I

    R = V I

    Onde:

    V = 115   V ;

    I = 10,86   A ;

    Logo:

    R = 115 10,86

    R = 10,58   Ω

    Passo 3

  3. Quanta energia térmica é produzida em 1   h pelo aquecedor?

Potência, por definição, é dada por:

P = Δ E Δ t

Δ E = P Δ t

Onde:

P = 1250   W ;

Δ t = 1   h = 3600   s ;

Logo:

Δ E = 1250 × 3600

Δ E = 4,5 × 10 6   J

Resposta

  1. I = 10,86   A ;
  2. R = 10,58   Ω ;
  3. Δ E = 4,5 × 10 6   J ;

Exercícios de Livros Relacionados

Os valores numéricos das tensões e correntes na interconexão apresentada na Figura P1.30 são dados na Tabela P1.30. A interconexão satisfaz o teste de potência?
O fabricante de uma pilha alcalina de lanterna, de 1,5 V, afirma que a pilha fornecerá 9 mA por 40 horas contínuas. Durante esse tempo, a tensão cairá de 1,5 V para 1,0 V. Suponha que a queda de tensã
A tensão e a corrente nos terminais do elemento de circuito da Figura 1.5 são mostradas nas figuras P1.27 (a) e (b). a) Desenhe o gráfico da potência versus t para 0 b) Calcule a energia fornecida ao
A tensão e a corrente nos terminais do elemento de circuito da Figura 1.5 são iguais a zero para t 0, elas são v = 3.200 t + 4 e - 1.000 t V, i = 128 t + 0 . 16 e - 1.000 t A.a) Em que instante a potê
A tensão e a corrente nos terminais do elemento de circuito da Figura 1.5 são iguais a zero para t 0, elas são v = 75 - 75 e - 1.000 t V, i = 50 e - 1.000 t mA. a) Determine o valor máximo da potência