Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 4.Problemas - Ex. 14
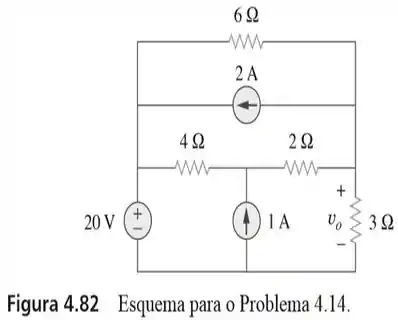
14. Aplique o princípio da superposição para determinar no circuito da figura
Passo 1
Olha só! No circuito da figura do enunciado, há a presença de três fontes independentes; duas fontes de tensão de e e uma fonte de corrente de .
Logo, usando superposição, temos que a tensão é dada pela soma das contribuições de tensão das três fontes individualmente. No caso, chamaremos de a contribuição da fonte de tensão, de a contribuição da fonte de corrente de e de a contribuição da fonte de corrente de .
Passo 2
Primeiro, vamos determinar . Para isso, vamos abrir o circuito no ramo onde está a fonte de corrente de e substituir a fonte de tensão por um curto circuito.
De modo que nosso circuito passa a ter a seguinte cara:
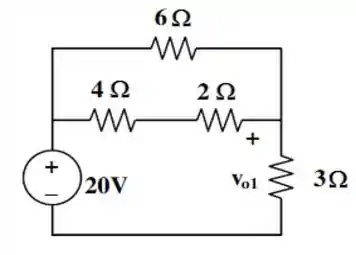
Nesse circuito, tiramos duas relações interessantes:
Onde por divisão de tensão, obtemos facilmente o valor de :
Passo 3
Em seguida, vamos determinar . Para isso, vamos substituir a fonte de corrente de por um circuito aberto, a fonte de tensão de por um curto circuito e bora deixar apenas a fonte de corrente de presente.
De modo que o circuito fica desse jeito aqui:
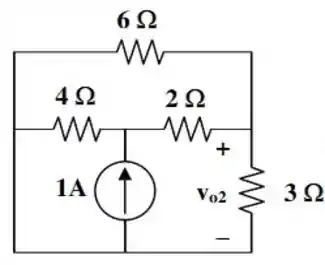
Vamos utilizar a transformação de fontes, para modificar aquela associação em paralelo entre a resistência de e a fonte de corrente de para uma associação em série entre uma fonte de tensão e a mesma resistêmcia.
Essa fonte de tensão é dada por:
E o nosso circuito fica desse jeito aqui embaixo...
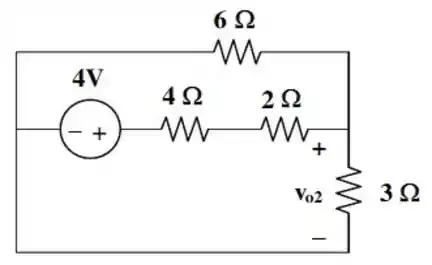
As resistência de e estão em paralelo.
E por divisão de tensão, temos que o valor de é dado por:
Passo 4
E por último, vamos determinar . Para isso, vamos substituir a fonte de corrente de por um circuito aberto, a fonte de tensão de por um curto circuito e deixar apenas a fonte de corrente de presente.
De modo que o circuito fica com essa tela aqui:
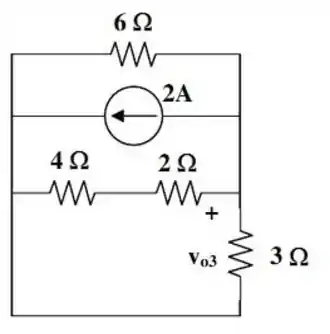
Nesse circuito, vemos que as resistências de e a associação em série entre e estão em paralelo.
Calculemos então, a resistência equivalente pra esse caso...
E com isso, nosso circuito pode ser modificado para a seguinte forma:
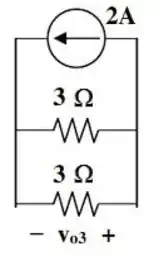
o valor de é dado pela multiplicação da resistência de pela corrente que pode ser facilmente obtida usando a divisão de corrente. Obtemos então, que...
O valor negativo, advém do fato de que ao passar pelo resistor, a corrente gera uma queda de tensão.
Pronto! Já temos as ferramentas que precisávamos.
Passo 5
Pra finalizar, basta somar , e e e encontraremos ...
Eureca! Resposta encontrada.