Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 11.Problemas - Ex. 17

17. Calcule o valor de Z L no circuito da figura 11.48 de modo que Z L receba a máxima potência média. Qual é a máxima potência média recebida por Z L ?

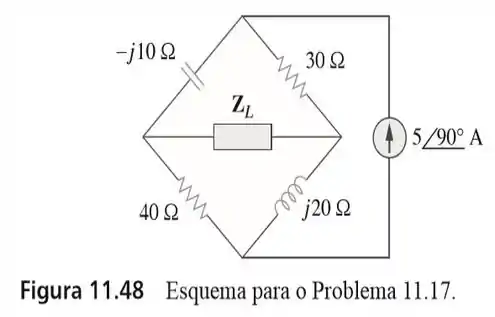
Passo 1

Olha só! O que temos que fazer é achar o equivalente de T h é v e n i n pra esse circuito.

Para isso, vamos abrir esse circuito no ramo onde está a fonte de corrente e tirar a impedância Z L . De modo que nosso circuito fica desse jeito aqui...

Z T h = 30 - j 10 | | 40 + j 20   Ω

Z T h = 30 - j 10 40 + j 20 30 - j 10 + 40 + j 20   Ω

Z T h = 30 - j 10 40 + j 20 70 + j 10   Ω

Z T h = 20   Ω

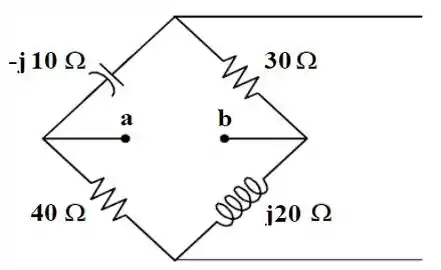
Bom! Obtemos a nossa impedância de T h é v e n i n .

Só que nossa análise não para por aqui. Essa impedância de T h é v e n i n vai ser justamente igual àquela impedância Z L do nosso circuito. Isso, para que ela receba a máxima potência média. Sendo assim:

Z L = 20   Ω

Passo 2

Agora, vamos concentrar nossas atenções na obtenção da tensão de T h é v e n i n . Para isso, bora prestar atenção na figura abaixo...

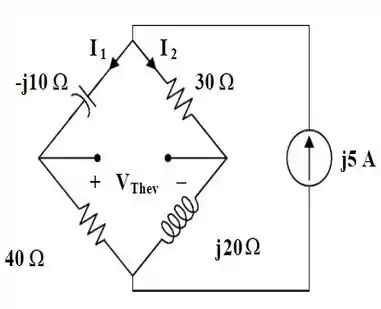
Usando divisão de corrente:

I 1 = 30 + j 20 30 + j 20 + 40 - j 10 ⋅ ( j 5 )   A

I 2 = 40 - j 10 30 + j 20 + 40 - j 10 ⋅ ( j 5 )   A

Obtemos que:

I 1 = 30 + j 20 30 + j 20 + 40 - j 10 ⋅ ( j 5 )   A

I 1 = 30 + j 20 70 + j 10 ⋅ ( j 5 )   A

I 1 = 10 13 ∠ 33,69 ° 10 50 ∠ 6,429 ° ⋅ ( 5 ∠ 90 ° )   A

I 1 = - 1,1 + j 2,3

I 2 = 40 - j 10 30 + j 20 + 40 - j 10 ⋅ ( j 5 )   A

I 2 = 40 - j 10 70 + j 10 ⋅ ( j 5 )   A

I 2 = 10 17 ∠ 33,69 ° 10 50 ∠ 6,429 ° ⋅ ( 5 ∠ 90 ° )   A

I 2 = 1,1 + j 2,7

E a tensão de T h é v e n i n , é dada por:

V T h = 30 I 2 + j 10 I 1

V T h = 30 ⋅ ( 1,1 + j 2,7 ) + j 10 ( - 1,1 + j 2,3 )

V T h = 10 + j 70

V T h = 10 50 ∠ 81,87 °

Passo 3

Pra finalizar e obter a máxima transferência de potência, basta usar a fórmula abaixo:

P m a x = | V T h | 2 2 Z T h + Z L 2 ⋅ Z L

Onde substituindo os valores numéricos, obtemos que...

P m a x = | 10 50 | 2 2 20 + 20 2 ⋅ 20

P m a x = 31,25   W

Resposta

P m a x = 31,25   W

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a leitura do wattímetro.
Calcule a leitura do wattímetro.
Dado i = i 1 + i 2 , onde i 1 = I 1 m cos ⁡ w 1 t i 2 = I 2 m cos ⁡ w 2 t É a corrente que flui no resistor R . Usando a definição do problema 12.13 , mostre, para w 1 ≠ w 2 , que P = P 1 + P 2 Onde P
Calcule o valor eficaz de uma corrente periódica para a qual um cicio e dado por:a) i = 3 tA 0 ≤ t ≤ 2 s 0 = 2t ≤ 4 s b) i = 6A0t2 s 0 = 2t8 s c) i = I m sin ⁡ 2 π t T A 0tT 2 0 = T 2tT s d) i = I m s
Mostre que, para 0 circuito do Ex. 15.4.1, a energia dissipada por ciclo e ∫ 0 2 π w 0 R I M 2 cos 2 ⁡ w 0 t d t = π R I M 2 w 0 e, desta forma, pela definição (15.27) e 0 resultado do Ex. 15.4.1. que