Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 11.Problemas - Ex. 19
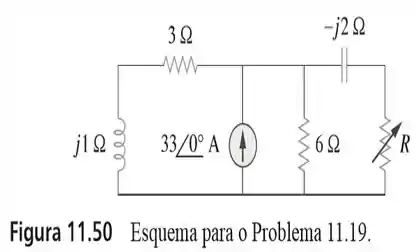
19. O resistor variável no circuito da figura é ajustado até ele absorver a máxima potência média. Determine e a máxima potência média absorvida.
Passo 1
Olha só! Primeiramente vamos descobrir a impedância de desse circuito.
Para isso, bora substituir a fonte de corrente por um circuito aberto.
De modo que nosso circuita fica do seguinte jeito:
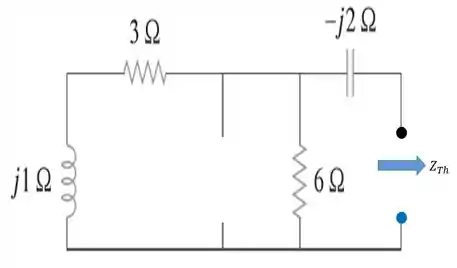
A impedância de , nesse caso, é dada por:
E como o resistor variável tem o mesmo módulo da impedância de . A única resposta possível é:
Passo 2
Agora, vamos calcular a impedância, que chamaremos de na parte esquerda do nosso circuito...
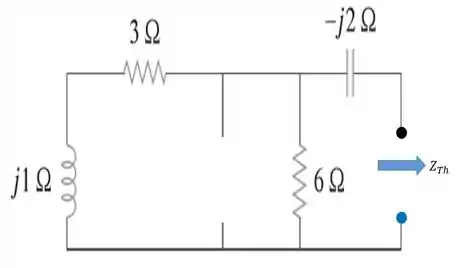
E uma vez que descobrimos o valor dessa impedância, fica fácil descobrir a tensão de , . Ela é dada pela produto da fonte de corrente por ...
Passo 3
Pra finalizar, vamos encontrar a máxima potência absorvida... Ela é dada por: