Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 16.Problemas - Ex. 4

Se , , qual o valor de que torna o circuito:

a) Superamortecido

b) Criticamente amortecido

c) Subamortecido

Passo 1

Beleza, temos aqui um circuito em série, certo? Podemos fazer a Lei de Kirchhoff das tensões nesse circuito e fazer a transformada de Laplace, isso vai nos dar:

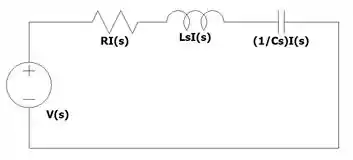
Substituindo os valores do enunciado:

Agora vamos colocar em evidência:

Multiplicando os dois lados por :

Passo 2

Os polos vão ser dados pelas raízes de , certo? Ou seja:

Agora, vamos lembrar um negócio:

Para o circuito ser superamortecido, os polos devem assumir valores reais e distintos

Para ser criticamente amortecido, os polos são iguais

Para ser subamortecido, os polos são complexos, sendo que um é o conjugado do outro

Fechou, bora lá testar esses polos :D

Passo 3

a) Para ser subamortecido, a raíz deve ser um número real, e pra que isso aconteça, o número dentro da raíz deve ser maior que 0, ou seja:

Passo 4

b) Para ser criticamente amortecido, a raíz deve ser 0, e pra que isso aconteça, o número dentro da raíz deve ser 0, ou seja:

Passo 5

c) Para ser subamortecido, a raíz deve ser um número complexo, e pra que isso aconteça, o número dentro da raíz deve ser negativo, ou seja:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A energia inicial no circuito da Figura P13.26 é nula. A fonte de tensão ideal é 600u(t) V. a) Determine Vo(s). b) Use os teoremas dos valores inicial e final para determinar vo(0+) e vo(q). c) Os val

Não há nenhuma energia armazenada no circuito da Figura P13.36 no instante em que a chave é fechada. a) Determine I1. b) Use os teoremas dos valores inicial e final para determinar i 1(0+) e i 1(q). c

As duas chaves no circuito da Figura P13.35 funcionam simultaneamente. Não há nenhuma energia armazenada no circuito no instante em que elas se fecham. Determine i(t), para t ≥ 0+, a partir do equival