Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 3.Problemas - Ex. 21

21. Para o circuito da figura 3.70 , determine v 1 e v 2 usando análise nodal.

Passo 1

No circuito acima os nós já estão identificados. O nó inferior está ligado ao terra e entre os nós 1 e 2 temos uma fonte de tensão de 3 v 0 . Vamos ver então, o que fazer para este caso:

Passo 2

Primeiramente, vamos escolher os sentidos das correntes e nomear as tensões de cada nó para aplicarmos a L K C :

Com isso, aplicando a L K C para o nó 1 , temos que:

∑ i   e n t r a m = ∑ i   s a e m

3   m A = i 0 + i 1

E depois, aplicando a L K C para o nó 2 , chegamos à:

∑ i   e n t r a m = ∑ i   s a e m

i 0 + i 1 = i 2

Passo 3

Nesse P a s s o ,vamos determinar agora as equações das correntes em relação às tensões nodais:

i 0 =   v 1 +   3 v 0 -   v 2 2000

i 1 =   v 1 -   v 2 4000

i 2 =   v 2   1000

E substituindo em seguida essas correntes, nas duas relações que obtivemos do L K C , chegamos ao seguinte sistema de equações:

0,003 =   v 1 +   3 v 0 -   v 2 2000 +   v 1 -   v 2 4000   ( I )   v 1 +   3 v 0 -   v 2 2000 +   v 1 -   v 2 4000 =   v 2   1000   ( I I )

Agora, vamos dar uma olhada de novo, na figura do P a s s o   1 :

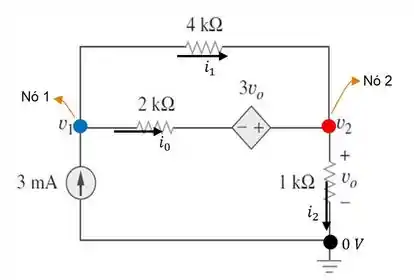
Ora bolas! A tensão nodal   v 2 é na verdade   v 0 . Sendo assim, nosso sistema de equações anterior vai ficar com a seguinte cara:

0,003 =   v 1 +   3 v 2 -   v 2 2000 +   v 1 -   v 2 4000   ( I )   v 1 +   3 v 2 -   v 2 2000 +   v 1 -   v 2 4000 =   v 2   1000   ( I I )

Simplificando...

v 1 +   v 2 = 4   ( I ) v 2 = 3 v 1   ( I I )

Passo 4

Uma vez que v 2 = 3 v 1 , bora substituir essa relação em ( I ) :

v 1 +   v 2 = 4

v 1 + 3 v 1 = 4

4 v 1 = 4

v 1 = 4 4   V

v 1 = 1   V

E depois, é só partir pro abraço pra obter v 2 :

v 2 = 3 v 1

v 2 = 3 ⋅ ( 1   V )

v 2 = 3   V

Resposta

v 1 = 1   V

v 2 = 3   V

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

23- Use o método das tensões de nó para determinar o valor de vo no circuito da Figura P4.23. Figura P4.23
32-a) Use o método das correntes de malha para determinar as correntes de ramo i a, i b e i c no circuito da Figura P4.32. b) Repita (a) com a polaridade da fonte de 140 V invertida. Figura P4.32
31-Mostre que, quando as equações 4.16, 4.17 e 4.19 são resolvidas para iB, o resultado é idêntico à Equação 2.25.
30-Use o método das tensões de nó para determinar a potência fornecida pela fonte de tensão de 20 V no circuito da Figura P4.30. Figura P4.30
29-Suponha que você seja um engenheiro projetista e alguém de sua equipe seja designado para analisar o circuito mostrado na Figura P4.29. O nó de referência e a numeração dos nós mostrados na figura