Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 11.Problemas - Ex. 21
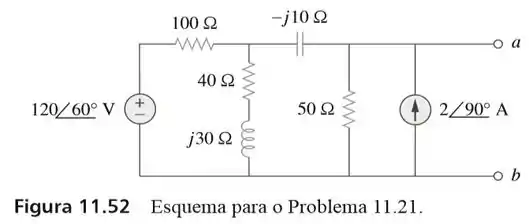
21. Suponha que a impedância da carga seja puramente resistiva, que carga deveria ser conectada aos terminais dos circuito da figura , de modo que seja transferida a potência máxima para a carga.
Passo 1
Olha só! Primeiramente, vamos descobrir a impedância de pra esse circuito.
Para isso, vamos substituir a fonte de tensão por um curto circuito e a fonte de corrente, por um circuito aberto.
Passo 2
De modo que o nosso circuito fica desse jeito aqui...
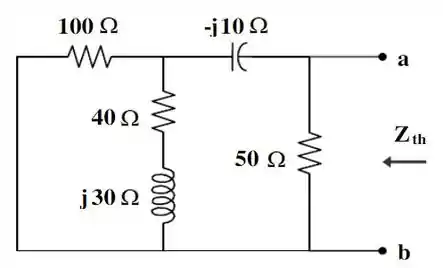
A impedância de , , pra esse circuito, é dada por:
E presta só atenção! Como a impedância da carga é puramente resistiva, a única carga possível a ser conectada é uma resistência, que chamaremos de .
Uma vez que resistências só tem a parte real... Não tem parte imaginária...
Logo, a carga vai ser dada pelo módulo de ...
E voilà! Resposta encontrada!