Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 11.Problemas - Ex. 77
77- Qual é a leitura do wattímetro no circuito da Figura .
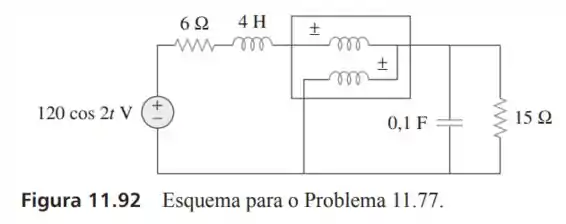
Passo 1
A fonte de tensão não está em mas vamos considerar a sua forma fasorial:
E o que essa fonte impõe ao circuito é de:
Então as reatâncias no indutor e no capacitor serão de:
Isso deixa nosso circuito da seguinte forma:
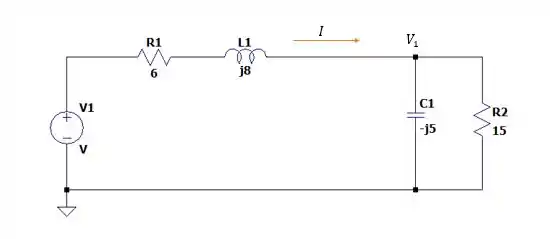
Onde temos que encontrar a tensão e a corrente que passam no nosso wattímetro e para facilitar a nossa conta vamos fazer a impedância equivalente entre o resistor de e a capacitância de .
Passo 2
Dessa forma a corrente correrá sobre todo o circuito e será igual a:
Dessa forma será igual a:
Passo 3
Então a potência complexa que passa sobre o wattímetro (lembrando que a fonte não está em é de):
Então a potência real que será mostrado no wattímetro é de:
Resposta
Exercícios de Livros Relacionados
17. Calcule o valor de Z L no circuito da figura 11.48 de modo que Z L receba a máxima potência média. Qual é a máxima potência média recebida por Z L ?
18. Determine o valor de Z L no circuito da figura 11.49 abaixo para a transferência de potência máxima.
19. O resistor variável R no circuito da figura 11.50 é ajustado até ele absorver a máxima potência média. Determine R e a máxima potência média absorvida.
21. Suponha que a impedância da carga seja puramente resistiva, que carga deveria ser conectada aos terminais a - b dos circuito da figura 11.52 , de modo que seja transferida a potência máxima para a
24. Determine o valor R M S da forma de onda mostrada na figura 11.55