Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 4.Problemas - Ex. 21
21- Usando a Figura , elabore um problema para ajudar outros estudantes a entender melhor a transformações de fontes.
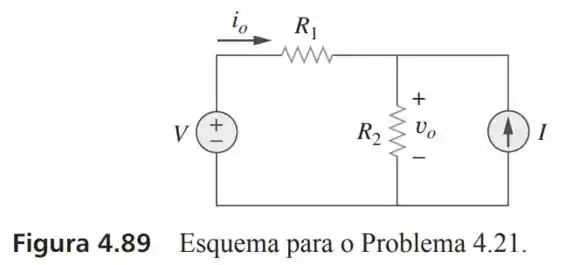
Passo 1
Vamos descobrir o valor de e de ao fazer:
Agora note que o resistor é o resistor ligado em série com a tensão , então podemos transformar essa fonte de tensão em uma fonte de corrente de valor:
Deixando nosso circuito da seguinte forma:
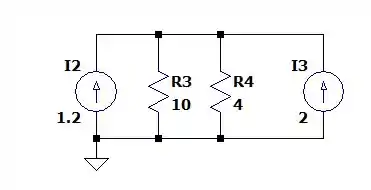
Como as fontes de tensão estão sujeitas as mesmas tensões então podemos somar as duas correntes da seguinte forma:
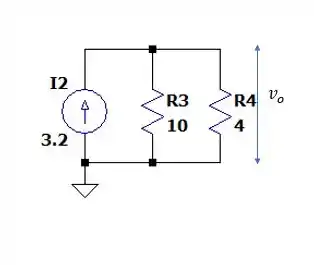
Então a corrente que passa pelo resistor de igual a (que será maior que na de ) será igual a:
Nos dando uma tensão igual a:
Não podemos dizer que será pois mudamos as condições iniciais de , de modo que agora a outra fonte irá atrapalhar nossa visualização.
Passo 2
Para encontrar vamos transformar a fonte de corrente em uma fonte de tensão por da seguinte forma:
Nos dando o seguinte circuito
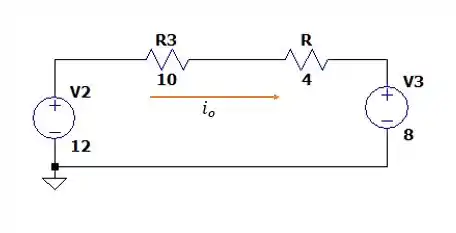
Assim como não podemos dizer agora que a tensão no resistor de é , pois a fonte ligada a ela mudou, mas a de não e é ela que vamos calcular.
Por diferença de tensão temos que: