Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 3.Problemas - Ex. 75
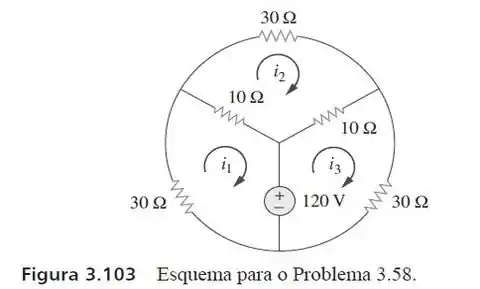
75. Use o ou o para resolver o problema
Passo 1
Olha só! A primeira coisa que precisamos fazer, é redesenhar esse circuito no como um circuito planar.
Para isso, vamos usar a ferramenta . Se forem seguidas as instruções fornecidas no tutorial (site) sobre criação de circuitos e análise CC, será gerado o esquema desse jeitinho aqui:
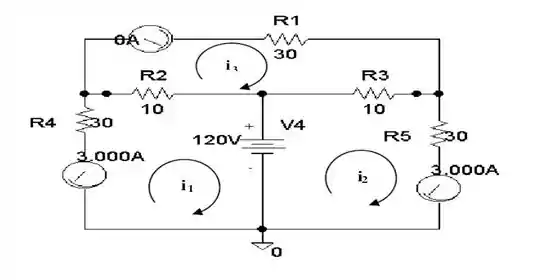
E aqui está a descrição dos seus elementos, a lista de ligações do esquema .
R_R4 $N_0002 $N_0001 30
R_R2 $N_0001 $N_0003 10
R_R1 $N_0005 $N_0004 30
R_R3 $N_0003 $N_0004 10
R_R5 $N_0006 $N_0004 30
V_V4 $N_0003 0 120V
v_V3 $N_0005 $N_0001 0
v_V2 0 $N_0006 0
v_V1 0 $N_0002 0
R_R4 $N_0002 $N_0001 30
R_R2 $N_0001 $N_0003 10
R_R1 $N_0005 $N_0004 30
R_R3 $N_0003 $N_0004 10
R_R5 $N_0006 $N_0004 30
V_V4 $N_0003 0 120V
v_V3 $N_0005 $N_0001 0
v_V2 0 $N_0006 0
v_V1 0 $N_0002 0
R_R4 $N_0002 $N_0001 30
R_R2 $N_0001 $N_0003 10
R_R1 $N_0005 $N_0004 30
R_R3 $N_0003 $N_0004 10
R_R5 $N_0006 $N_0004 30
V_V4 $N_0003 0 120V
v_V3 $N_0005 $N_0001 0
v_V2 0 $N_0006 0
v_V1 0 $N_0002 0
R_R4 $N_0002 $N_0001 30
R_R2 $N_0001 $N_0003 10
R_R1 $N_0005 $N_0004 30
R_R3 $N_0003 $N_0004 10
R_R5 $N_0006 $N_0004 30
V_V4 $N_0003 0 120V
v_V3 $N_0005 $N_0001 0
v_V2 0 $N_0006 0
v_V1 0 $N_0002 0
R_R4 $N_0002 $N_0001 30
R_R2 $N_0001 $N_0003 10
R_R1 $N_0005 $N_0004 30
R_R3 $N_0003 $N_0004 10
R_R5 $N_0006 $N_0004 30
V_V4 $N_0003 0 120V
v_V3 $N_0005 $N_0001 0
v_V2 0 $N_0006 0
v_V1 0 $N_0002 0
De modo a poder mostrar as correntes necessárias, inserimos pseudocomponentes nas malhas apropriadas. O esquema é salvo e simulado selecionando-se .
Passo 2
Depois, disso o próprio software vai compilar por um tempo e ele mesmo irá nos forrecer o valor das correntes de malha, que são: