Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 10.Problemas - Ex. 25

25. Determine i 0 no circuito abaixo, usando análise de malhas.

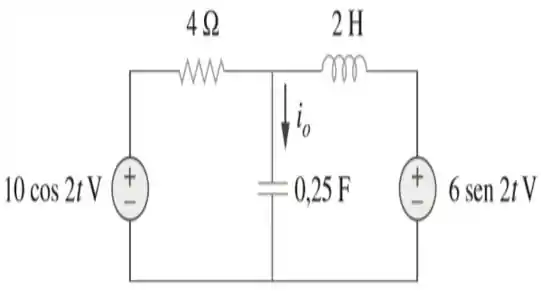
Passo 1

Fala galerinha! Vamos pra mais um problema sobre regime estacionário em circuito senoidal.

Olha só! A primeira coisa que precisamos fazer, é passar os elementos do circuito para o domínio da frequência, ou seja, para a forma fasorial.

10 cos ⁡ 2 t = 10 cos ⁡ ( 2 t ) = 10 ∠ 0 °     ,   ω = 2   r a d / s

10 cos ⁡ 2 t = 10 ∠ 0 °     ,   ω = 2   r a d / s

6 sen ⁡ 2 t = 6 cos ⁡ ( 2 t - 90 ° ) = 6 ∠ - 90 °     ,   ω = 2   r a d / s

6 sen ⁡ 2 t = 6 ∠ - 90 °     ,   ω = 2   r a d / s

2   H → j ω L = j 2 ⋅ 2 = j 4   Ω

1   F → - j 1 ω C = - j 1 2 ⋅ 0,25 = - j 2   Ω

Passo 2

Agora, vamos preparar o circuito pra utilizar a nossa análise de malhas. Os elementos do circuito, já devem estar atualizados no domínio da frequência.

E aqui está, na nossa bela imagem, o circuito reformulado:

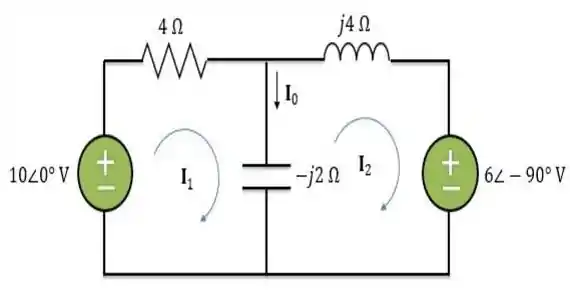
Aplicando a lei das tensões de K i r c h h o f f ( L K T ) para a malha 1 , alcançamos a seguinte igualdade:

- 10 + 4 I 1 - j 2 I 1 - I 2 = 0

- 10   - j 2 I 1 + j 2 I 2 + 4 I 1 = 0

- j 2 I 1 + j 2 I 2 + 4 I 1 = 10

4 - j 2 I 1 + j 2 I 2 = 10   ( I )

E depois, fazendo a L K T para a malha 2 , chegamos à:

- j 6 - j 2 I 2 - I 1 + j 4 I 2 = 0

j 2 I 1 + j 2 I 2 = j 6   ( I I )

Dividimos essa equação ( I I ) por j 2 , e obtemos que:

j 2 I 1 + j 2 I 2 = j 6   ( I I )

I 1 + I 2 = 3   ( I I )

Passo 3

Chegamos assim, ao seguinte sistema:

4 - j 2 I 1 + j 2 I 2 = 10   ( I ) I 1 + I 2 = 3   ( I I )

Isolando I 2 na segunda equação e substituindo na primeira, temos:

4 - j 2 I 1 + j 2 I 2 = 10  

4 - j 2 I 1 + j 2 ( 3 - I 1 ) = 10  

4 - j 2 I 1 + j 6 - j I 1 = 10

4 - j 4 I 1 = 10 - j 6

I 1 = 10 - j 6 4 - j 4

Passando para a forma polar essa corrente, obtemos que:

I 1 = 10 2 + ( - 6 ) 2 ∠ tan - 1 ⁡ - 6 10   4 2 + ( - 4 ) 2 ∠ tan - 1 ⁡ - 4 4

I 1 = 11,66 ∠ - 30,96 ° 5,66 ∠ - 45 °   A

I 1 = 2,06 ∠ 14,04 °   A

E o valor de I 2 é igual a:

I 2 = 3 - I 1

I 2 = 3 - 2,06 ∠ 14,04 °  

I 2 = 3 - ( 2 + j 0,5 )

I 2 = 1 - j 0,5   A

Falta achar o valor de i 0 . Ora bolas! Analisando, o circuito podemos ver que i 0 é dado por:

i 0 = I 1 - I 2

i 0 = 2 + j 0,5 - ( 1 - j 0,5   )

i 0 = 1 + j

i 0 = 1,414 ∠ 45 °   A

Pra finalizar, bora botar a corrente no domínio do tempo:

i 0 = 1,414 cos ⁡ ( 2 t + 45 ° )   A  

Resposta

i 0 = 1,414 cos ⁡ ( 2 t + 45 ° )   A  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

No circuito da Figura 10.46, a corrente i(t) é: 10 cos ⁡ tA b) 10 s e ntA c) 5 cos ⁡ tA d) 5s e ntA e) 4.472 cos ⁡ t - 63.43 ° A
O valor da corrente I 0 no capacitor da Figura 10.44 é: 4 ∠ 0 °A b) 2.4 ∠ - 90 °A c) 0.6 ∠ 0 ° Ad) - 1A
Determine i no circuito da Figura 10.50.
Usando a Figura 10.51, elabore um problema para ajudar outros estudantes a entender melhor a análise nodal.
Determine V o no circuito da Figura 10.52.