Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 10.Problemas - Ex. 23
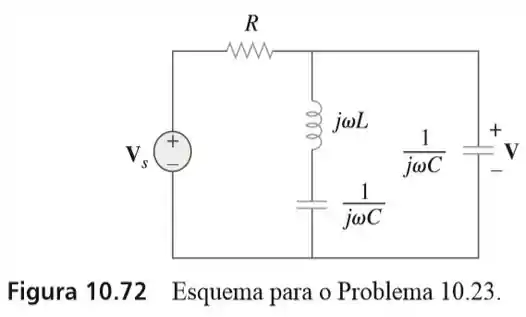
23. Usando a análise nodal, obtenha no circuito da figura
Passo 1
Fala galerinha! Vamos pra mais um problema sobre regime estacionário em circuito senoidal.
Bom! A questão nos diz que vamos ter que usar a análise nodal pra resolver esse problema.
Pois então, é extamente isso que a gente vai fazer. Bora fazer o esboço desse circuito, dando nomes aos bois. Isto é, desenhar os sentidos das correntes de cada nó e nomear as tensões de cada nó para aplicar a .
Ah! Nosso circuito tem dois nós, hein!?
E aqui está nossa figura:
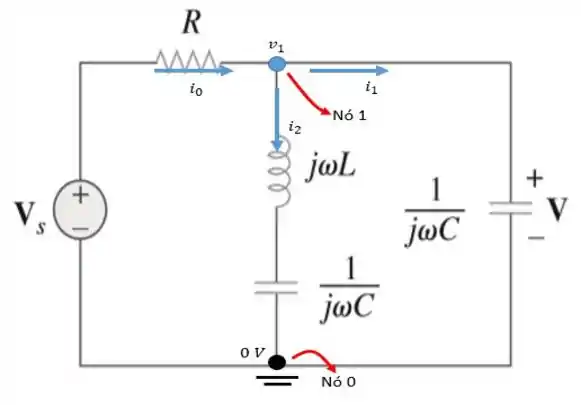
Aplicando a lei das correntes de para o nó , obtemos a seguinte igualdade:
E essas correntes são dadas em função das tensões nodais, por:
Passo 2
Substituindo esses valores das correntes em função das tensões nodais, na fórmula que obtemos usando o :
Agora, bora parar um pouco pra raciocionar! A tensão nodal , não é a mesma coisa que ?
Sim, senhor! As duas são a mesmo coisa! Desse modo, nossa relação de antes vai ficar assim:
Trabalhando em cima dessa expressão, iremos obter nossa resposta:
Demorou, mas chegou! Encontramos nossa resposta!