Enunciado
Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 4.Problemas - Ex. 33
33-
Resolva o Problema 4.11 usando o método das correntes de malha.
Passo 1
Então, vamos enfrentar essa fera... brincadeira rsrs. Essa questão é suave na nave, basta que a gente pense um pouquinho, vamos nessa?!
Usando o circuito da figura 4.11 podemos resolver essa.
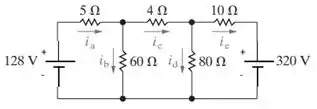
Figura 4.11
a)
As três equações de corrente de malha são:
−128 + 5ia + 60(ia − ic) = 0
4ic + 80(ic − ie) + 60(ic − ia) = 0
320 + 80(ie − ic) + 10ie = 0
Passo 2
Passando as equações para a forma padrão:
ia(5 + 60) + ic(−60) + ie(0) = 128
ia(−60) + ic(4 + 80 + 60) + ie(−80) = 0
ia(0) + ic(−80) + ie(80 + 10) = −320
Após resolvermos, temos:
ia = −6.8 A;
ic = −9.5 A;
ie = −12 A.
Passo 3
Agora calculando as correntes restantes do ramo:
ib = ia − ic = 2.7 A
id = iv − ie = 2.5 A
Passo 4
b)
p128V = −(128)*(−6.8) = 870.4 W (consumida)
p320V = (320)*(−12) = −3840 W (fornecida)
Portanto, a potência total desenvolvida é 3840 W.
Resposta
a)ia = −6.8 A;
ic = −9.5 A;
ie = −12 A
b) 3840 W