Enunciado
Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 4.Problemas - Ex. 58
A fonte variável de corrente cc no circuito da Figura P4.58 é ajustada de modo que seja igual a zero.
a) Você usaria o método das tensões de nó ou das correntes de malha para determinar ? Explique sua escolha.
b) b) Use o método selecionado em (a) para determinar .
c) Verifique sua solução mostrando que a potência gerada é igual à potência dissipada.
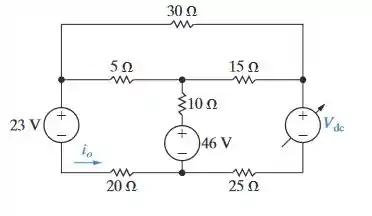
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!
A - O método atual de malha é a ferramenta preferida para encontrar , como o elemento desconhecido é uma fonte de tensão e, portanto, a equação da malha de torção teria diretamente nela como um desconhecido.
B – Escrevendo a LKT para a malha esquerda, nós temos que
Ou
Para a malha da direita, nós temos que
Simplificando
Passo 2
Escrevendo a lei das tensões de Kirchoff na malha mais externa,
Ou
Resolvendo os termos, nós temos que
Passo 3
C - Calculando a potência fornecida
Substituindo os valores,
Para a fonte de
Novamente, fazendo a substituição
E no caso da fonte variável ,
Substituindo
Logo, a potência total fornecida
Passo 4
Agora vamos lá, para o cálculo da potência dissipada, vamos ter que calcular para cada resistor, então vamos dar uma respirada, um, dois, três e vamos responder!
Fazendo a substituição
Para o resistor de
Com isso, nós temos que
Para o resistor de
Substituindo os termos
Para o resistor de , temos os seguintes resultados
Então, a potência total dissipada é igual a
Com isso, é igual a