Enunciado
Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 4.Problemas - Ex. 36
36-
a) Use o método das correntes de malha para determinar a potência total gerada no circuito da Figura P4.36.
b) Verifique sua resposta mostrando que a potência total gerada é igual à potência total dissipada.
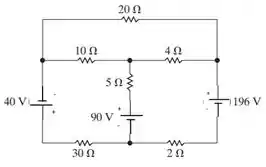
Figura P4.36
Passo 1
Então, vamos enfrentar essa fera... brincadeira rsrs. Essa questão é suave na nave, basta que a gente pense um pouquinho, vamos nessa?!
a)
40 + 10(i1 − i2) + 5(i1 − i3) + 90 + 30i1 = 0
20i2 + 4(i2 − i3) + 10(i2 − i1) = 0
196 + 2i3 − 90 + 5(i3 − i1) + 4(i3 − i2) = 0
Passo 2
Após resolver as equações do passo anterior, temos os seguintes resultados:
i1 = −5 A;
i2 = −3 A;
i3 = −13 A
Agora a gente calcula as potências:
p40 = 40i1 = −200W (fornecida)
p90 = 90(i1 − i3) = 720W (consumida)
p196 = 196i3 = −2548W (fornecida)
∑pfornecida = 2748W
Passo 3
b) Agora a gente encontra a resposta mostrando que a potência total fornecida é igual à potência total consumida.
p20Ω = (−3)2*(20) = 180W
p10Ω = (2) 2*(10) = 40W
p4Ω = (10) 2*(4) = 400W
p5Ω = (8) 2*(5) = 320W
p30Ω = (−5) 2*(30) = 750W
p2Ω = (−13) 2*(2) = 338W
∑pconsumida = 720 + 180 + 40 + 400 + 320 + 750 + 338 = 2748W
Resposta
a) ∑pfornecida = 2748W
b) ∑pfornecida = 2748W