Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 3.Problemas - Ex. 37
37. Resolva o problema , usando análise de malhas.
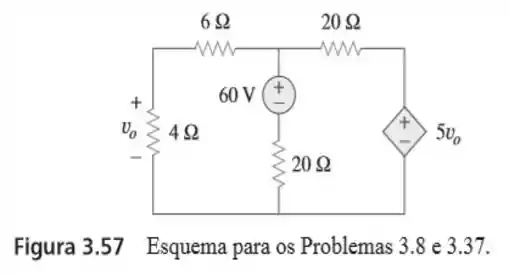
Passo 1
Bom! Se estamos trabalhando com análise de malhas, então temos que nomear as correntes de malha do nosso circuito.
Por isso, vamos fazer o esboço desse circuito, já com as correntes de malha indicadas:
E agora, assumindo que as correntes e estão em ; vamos finalmente aplicar a análise de malhas pra esse nosso circuito.
Bora primeiro percorrer a malha . O objetivo é determinar as tensões nessa malha. E para isso, consideremos as quedas de tensão como positivo e as elevações de tensão como negativo...
Passo 2
Em seguida, bora percorrer a malha . Novamente, vamos repetir o mesmo procedimento adotado do :
Essa tensão é o produto da corrente de malha pela resistência de , como podemos ver na figura anterior. Só que nesse caso, como a corrente de malha circula no sentido anti-horário; há uma elevação de tensão. Sendo assim...
Passo 3
Alcançamos assim, o seguinte par de equações:
Somando as duas equações, obtemos que:
E o valor de é dado por:
Pra finalizar! Como já mencionamos antes, a nossa tensão é dada por:
Missão cumprida! Encontramos nossa resposta!