Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 3.Problemas - Ex. 38
38. Aplique análise de malhas ao circuito da Figura e obtenha .
Passo 1
Bom! Se estamos trabalhando com análise de malhas, então temos que nomear as correntes de malha de cada uma das quatro malhas do nosso circuito.
Por isso, vamos fazer o esboço desse circuito, já com as correntes de malha indicadas:
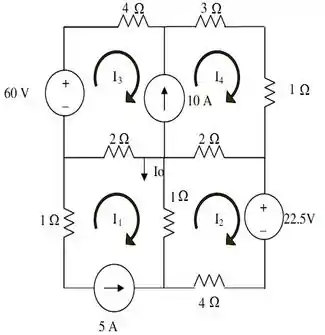
E agora, vamos finalmente aplicar a análise de malhas pra esse nosso circuito.
Bora primeiro percorrer a malha . Olha só! Pra nossa imensa felicidade, já temos a corrente de malha pra essa parte. Ela vai valer:
é negativa, porque percorre um caminho contrário ao do verdadeiro sentido da corrente.
Passo 2
Em seguida, bora percorrer a malha . O objetivo aqui, é determinar as tensões nessa malha. E para isso, consideremos as quedas de tensão como positivo e as elevações de tensão como negativo...
Passo 3
Entre as malhas e , existe uma supermalha. Isso quer dizer que devemos excluir aquela fonte de corrente de e considerar as duas malhas como se fossem uma só.
Vamos expandir as multiplicações agora:
E agora vamos juntar as mesmas variáveis:
E pela supermalha, também tiramos que:
Passo 4
Obtemos assim, o seguinte sistema de equações:
Bom! A questão pede pra gente resolver esse problema com o uso do . Mas como não temos , vamos apelar pro mesmo, que é bastante parecido. Afinal, praticidade é tudo que a gente quer, né não?
Olhas só! Esse sistema de três equações e três incógnitas pode ser escrito na forma matricial, como:
Ou seja, o sistema pode ser escrito em função de três matrizes. Vamos dar nomes a elas...
Sabe uma coisa legal de trabalhar com sistemas lineares em matrizes. Para obter a solução desse sistema linear, basta usar a seguinte relação:
Passo 5
Agora, vamos fazer isso como no . A matriz vai ser escrita assim, nesse software...
E a matriz fica desse jeito...
Fazendo , podemos obter nossa resposta...
Desse jeitinho aqui:
Por fim! A questão nos pede para obter o valor de .
Ora bolas! Pela figura do , podemos ver que:
E voilà! Encontramos nossa resposta!