Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 10.Problemas - Ex. 43
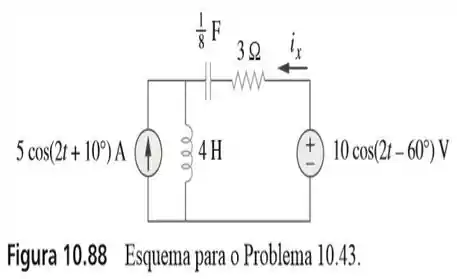
43. Usando o princípio da superposição, determine no circuito da figura
Passo 1
Fala galerinha! Bora pro nosso segundo probleminha sobre superposição em circuitos .
Como podemos ver, todos os elementos desses circuito estão na mesma frequência, igual a . O diferencial dessa questão, é que há a presença de duas fontes, uma fonte de corrente e uma fonte de tensão.
Por isso, antes de qualquer coisa, vamos passar todos os elementos desse circuito pro domínio da frequência:
Tendo feito isto, vamos finalmente usar a superposição. Para isso, bora separar individualmente cada fonte presente no circuito, no caso, a fonte de corrente e a de tensão.
Iremos calcular a corrente naquele ramo do circuito proveniente apenas da fonte de tensão,. Depois, calcularemos a corrente proveniente apenas da contribuição da fonte de corrente. Somamos as duas e, como resultado obtemos .
Vamos lá! Mão na massa!
Passo 2
Bora começar! Inicialmente, iremos considerar apenas a contribuição da fonte de tensão. Nesse caso, teremos que abrir o circuito no ramo onde está a fonte de corrente.
Desse jeitinho aqui:
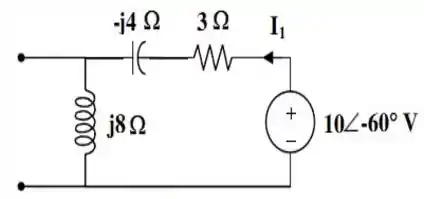
E a corrente , nesse caso, é dada por:
Vamos deixar desse jeito mesmo! Já já entenderemos o porquê disso.
Passo 3
Agora, vamos considerar apenas a fonte de corrente. Logo, a fonte de tensão alternada vai virar um curto circuito.
Desse modo, o nosso circuito vai ficar com a seguinte cara:
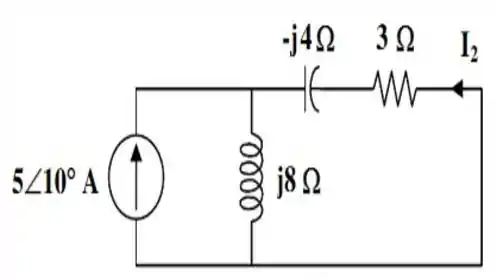
E a corrente pode então, ser facilmente obtida por divisão de corrente pelo seguinte cálculo abaixo...
Esse sinal negativo advém do fato, de que na divisão de corrrente, a corrente de , ao chegar do nó, irá se dividir em duas. Ou seja, pelo menos teoricamente, a corrente vai sair do nó e não entrar, como na nossa figura. Continuando com os cálculos...
Viu só! As duas correntes tem a parte no denominador.
Passo 4
Pra finalizar, vamos somar essas correntes a fim de obter :
Falta só passar pro domínio da frequência:
Pronto! Missão cumprida!