Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 10.Problemas - Ex. 61

Determine o circuito equivalente de Thévenin nos terminais a-b do circuito da Figura 10.104.

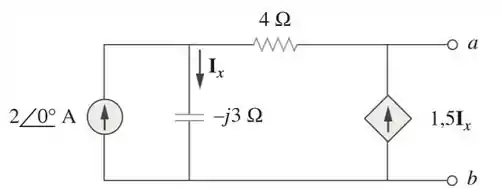
Passo 1

Primeiro, resolvemos a tensão do circuito aberto usando o circuito acima e escrevendo equações de dois nós. Então resolvemos a corrente de curto-circuito que precisa apenas da equação de um nó. Para poder resolver o V o c , precisamos resolver essas três equações,

- 2 + V 1 - 0 j 3 + V 1 - V o c 4 = 0   e V o c - V 1 4 - 1.5 I x = 0

Onde

I x = V 1 - 0 - j 3

Para resolver a corrente I s c , precisamos resolver essas 3 equações:

- 2 + V 2 - 0 - j 3 + V 2 - 0 4 = 0 ,     I s c = V 2 4 + 1.5 I x

I x = V 2 - j 3

E finalmente, V t h = V o c e Z e q = V o c I s c

Passo 2

Agora vamos atrás das variáveis que ficaram! Para V o c , temos que:

I x = j . 0333 V 1   e   0.25 + 1.5 j 0.333 V 1 = 0.25   V o c

Portanto,

V 1 = 0.447 ∠ - 63.43 ° V o c ,     O q u e   n o s   l e v a   a

0.25 + j 0.333 V 1 - 0.25   V o c = 2

Ou seja,

V o c = 26.83 ∠ 153.44 °   V

Passo 3

E vamos continuar! Para I s c ,

I s c = V 2 4 + 1.5 I x = 0.25 + j 0.33 V 2

V 2 - 0 - j 3 + V 2 - 0 4 = 2 = 0.25 + j 0.33 V 2

V 2 = 4.8 ∠ - 53.13 °

Voltando,

I s c = 0.25 + j 0.5 V 2 = 2.6832 ∠ 10.305 ° A

Portanto,

Z e q = V o c I s c = 10 ∠ 143.13 ° Ω

Resposta

Z e q = 10 ∠ 143.13 ° Ω

V t h = V o c = 26.83 ∠ 153.44 °   V

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

44. Use o princípio da superposição para obter v x no circuito da figura 10.89 . Seja v s = 50 sen ⁡ 2 tV e i s = 12 cos ⁡ ( 6 t + 10 ° )A .
43. Usando o princípio da superposição, determine i x no circuito da figura 10.88
45. Use superposição para determinar i ( t ) no circuito da figura 10.90
46. Determine v 0 ( t ) no circuito da figura 10.91 usando o princípio da superposição.
47. Determine i 0 no circuito da figura 10.92 utilizando o princípio da superposição.