Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 10.Problemas - Ex. 42
42. Considere a Figura e elabore um problema para ajudar outros estudantes a entender melhor o teorema da superposição.
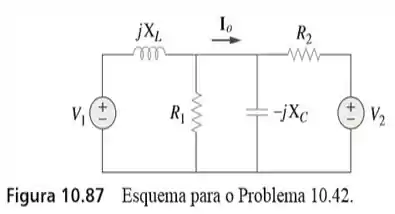
Passo 1
Fala galerinha! Bora resolver mais um probleminha sobre superposição em circuitos .
Olha só! Como é um problema que nós mesmos temos que elaborar... A primeira coisa a se fazer, é atribuir alguns valores aleatórios para os elementos desse circuito. Vamos lá!!
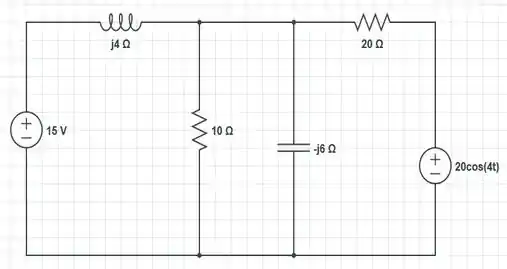
Nessa figura que esboçamos; há a presença de uma fonte de tensão de corrente contínua e outra de corrente alternada.
O que precisamos fazer pra esse caso, é calcular separadamente as contribuições de cada fonte de tensão e depois somar as duas.
Quando digo contribuições, é somar a corrente naquele ramo do circuito gerada apenas pela fonte de tensão , com a corrente originada apenas pela fonte de tensão .
Vamos lá! Mãos à obra!
Passo 2
Inicialmente, vamos excluir a fonte de tensão e deixar apenas a fonte de tensão em corrente contínua .
Desse modo, o indutor vai se comportar como um curto circuito e o capacitor como um circuito aberto.
E o nosso circuito vai ficar então, com a seguinte cara:
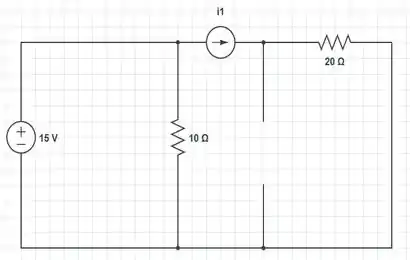
A corrente circulante no ramo que é o nosso alvo nesse circuito, iremos chamar de ...
E uma vez que os resistores de e estão submetidos à mesma diferença de potencial, logo:
Passo 3
Agora, vamos tomar o caminho inverso. Excluimos a fonte de tensão e deixar apenas a fonte de tensão alternada .
Antes, vamos passar os elementos pro domínio da frequência:
Desse modo, o nosso circuito pode ser representado pela seguinte imagem:
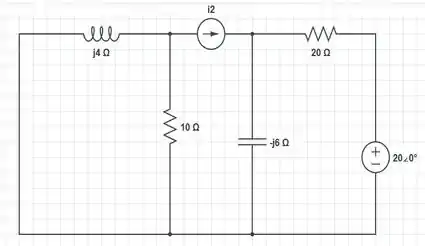
Em seguida, bora aplicar uma transformação de fontes nessa parte que inclui o resistor de e a fonte de tensão de . Ficaremos com uma fonte de corrente e o mesmo resistor em paralelo:
Desse jeitinho aqui:
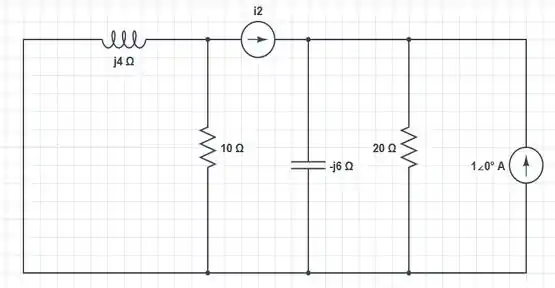
E novamente fazendo uso da divisão de corrente, obtemos que é dada por:
Só falta passar para o domínio do tempo:
Passo 4
Pra finalizar, basta somar as correntes e e iremos obter o valor da corrente :
Missão cumprida!