Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 10.Problemas - Ex. 45
45. Use superposição para determinar no circuito da figura
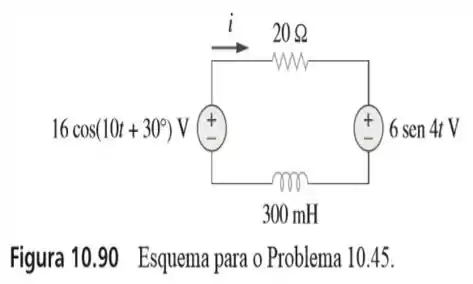
Passo 1
Fala galerinha! Bora pra mais um probleminha sobre superposição em circuitos .
Olha só! Na figura do enunciado, há a presença de duas fontes de tensão alternada, só que em frequência diferentes
O que precisamos fazer pra esse caso, é analisar a influência isolada de cada fonte no circuito. Ou seja, iremos considerar cada fonte separadamente, e a corrente elétrica total em qualquer ramo do circuito é igual a soma algébrica das tensões produzidas por cada fonte atuando separadamente.
Ou seja, bora chamar de a corrente no circuito apenas com a fonte de e , a corrente no circuito com a tensão de . Depois, somaremos a duas para obter .
Vamos então, por a mão na massa.
Passo 2
Primeiramente, vamos retirar a fonte de tensão alternada da direita.
E passar os elementos pro domínio da frequência:
Nosso circuito, tem então, a seguinte cara:
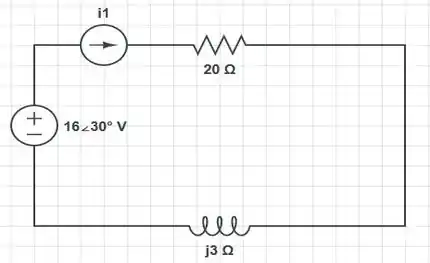
Já que temos apenas uma malha. Para achar a corrente , basta dividir a tensão pela impedância equivalente nesse circuito:
Passando essa corrente pro domínio do tempo...
Passo 3
Agora, vamos excluir a fonte de tensão alternada localizada à esquerda do circuito na figura do enunciado.
E já sabe, né! Primeira coisa a se fazer é passar os elementos pro domínio da frequência:
Olha! Eu sei que seria legal fazer o esboço de como ficaria o circuito pra esse caso. Mas tá na cara que vai ser do mesmo jeito que no . Basta dividir a tensão equivalente pela impedância total, composta pelo resistor e pelo indutor de . Sendo assim, a corrente é dada por:
O sinal negativo, advém do fato que ao passar pela fonte de tensão, a corrente gera uma queda de tensão. Voltando aos cálculos...
Passando para o domínio do tempo...
Passo 4
Por fim, temos apenas que somar as correntes e para obter a corrente :