Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 3.Problemas - Ex. 45
45. Determine a corrente no circuito da figura .
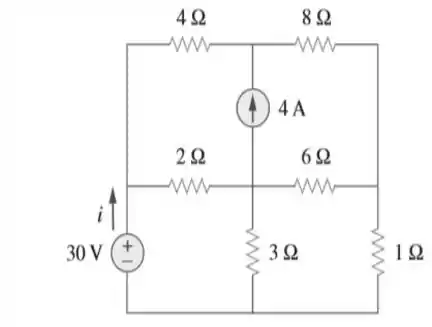
Passo 1
Olha só! Temos nesse circuito a presença de uma supermalha, como indicado na figura abaixo:
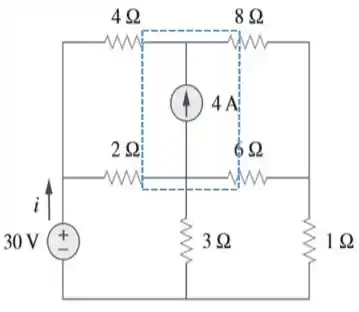
Baseado nisso, a primeira coisa que temos que fazer é o esboço desse circuito com as correntes de malha que nele estão presentes...
Obtemos então, a seguinte imagem:
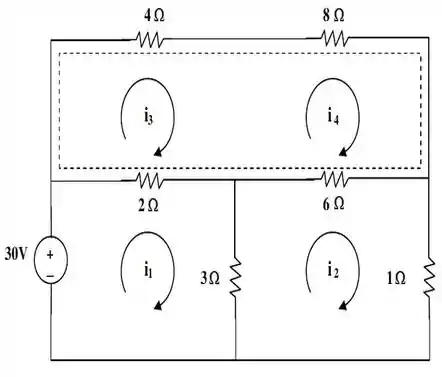
E com isso, vamos à análise das malhas.
Bora primeiro percorrer a malha . Olha só! O objetivo aqui, é determinar as tensões nessa malha. E para isso, consideremos as quedas de tensão como positivo e as elevações de tensão como negativo. A soma disso tudo tem que dar zero...
Passo 2
Em seguida, bora percorrer a malha . Repetindo o mesmo procedimento do , obtemos que...
Passo 3
E por fim, vamos percorrer a supermalha; de modo que obtemos a seguinte igualdade:
Só que desse supermalha também tiramos uma relação interessante. Por lei de , obtemos que:
Passo 4
Obtemos assim, o seguinte sistema de equações:
Bom! Essa questão aqui, a gente com certeza vai precisar usar o . Mas só que como a gente não tem o , vamos usar um software parecido, que é o .
Olha só! Esse sistema de quatro equações e quatro incógnitas pode ser escrito na forma matricial, como:
Ou seja, o sistema pode ser escrito em função de três matrizes. Vamos dar nomes a elas...
Sabe uma coisa legal de trabalhar com sistemas lineares em matrizes. Para obter a solução desse sistema linear, basta usar a seguinte relação:
Resumindo... As quatro soluções desse sistema são dadas pelo produto da inversa da matriz pela matriz . Que maravilha, não? Já pensou em fazer esse cálculo aqui! O tamanho que ia ficar! Cruz-credo!
Passo 5
Agora, vamos fazer isso como no . A matriz vai ser escrita nesse software assim...
E a matriz fica desse jeito...
Fazendo , podemos obter nossa resposta...
Desse jeitinho aqui:
E pronto! Obtemos nossas quatro correntes, iguais à:
A questão nos pede para determinar a corrente no circuito. Só que nós já obtemos, rapaz!
Ora bolas! A corrente , na verdade é a corrente de malha , como podemos ver comparando o circuito do com o do enunciado. Sendo assim, nossa resposta é...