Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 3.Problemas - Ex. 46
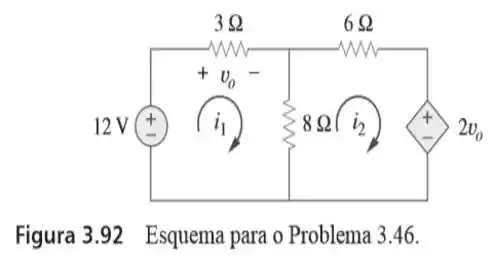
46. Calcule as correntes de malha e na figura
Passo 1
Bom! Bora logo pro que interessa e fazer a análise de malhas para esse nosso circuito.
Bora primeiro percorrer a malha . Olha só! O objetivo aqui, é determinar as tensões nessa malha. E para isso, consideremos as quedas de tensão como positivo e as elevações de tensão como negativo. A soma disso tudo tem que dar zero...
Passo 2
Em seguida, bora percorrer a malha . Repetindo o mesmo procedimento do , obtemos que:
E esse aí? Como é que nós vamos ajeitar ele?
Ora bolas! Tá na cara! Basta olhar a figura do enunciado e ver que a tensão é dada pelo produto da resistência de pela corrente de malha . Sendo assim, ficamos com uma nova igualdade...
Passo 3
E substituindo essa igualdade na equação que obtemos no , chegamos a seguinte resultado:
A corrente de malha , por sua vez, é dada por:
Viu só! Foi moleza! Encontramos nossas respostas numa tacada só!