Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 10.Problemas - Ex. 47
47. Determine no circuito da figura utilizando o princípio da superposição.
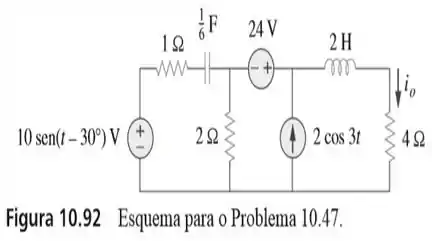
Passo 1
Fala galerinha! Bora pro nosso segundo probleminha sobre superposição em circuitos .
Olha só! Na figura do enunciado, há a presença de uma fonte de corrente alternada, uma fonte de tensão contínua e outra fonte de tensão alternada.
O que precisamos fazer pra esse caso, é analisar a influência isolada de cada fonte no circuito. Ou seja, iremos considerar cada fonte separadamente, e a corrente elétrica total em qualquer ramo do circuito é igual a soma algébrica das tensões produzidas por cada fonte atuando separadamente.
Vamos então, por a mão na massa.
Passo 2
Primeiramente, vamos retirar a fonte de tensão alternada e abrir o circuito no ramo onde está a fonte de corrente, como manda o protocolo.
Desse modo, uma vez que estamos operando em tensão contínua, o capacitor vira um circuito aberto, e o indutor vira um curto circuito.
A seguinte figura abaixo, ilustra isso:
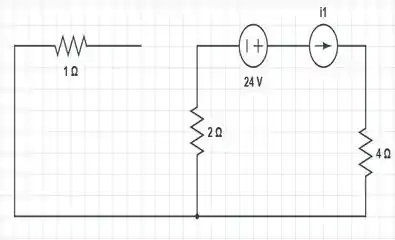
E como a corrente desse caso, que chamamos de , está circulando apenas naquela malha à direita... Logo, é fácil determinar seu valor:
Passo 3
Agora, vamos excluir a fonte de tensão alternada e a fonte de tensão contínua, deixando apenas a fonte de corrente alternada.
E já sabe, né! Primeira coisa a se fazer é passar os elementos pro domínio da frequência:
Desse modo, o nosso circuito vai ficar com a seguinte cara:
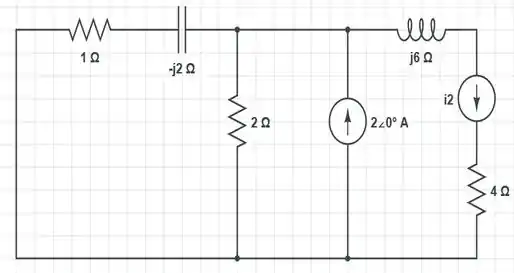
O resistor de e o indutor de impedância , estão em série. E o resultado dessa associação, está em paralelo com o resistor de . De forma que temos...
E a corrente pode então, ser facilmente obtida por divisão de corrente. Desse jeitinho aqui:
Passando pro domínio do tempo...
Passo 4
E por último, vamos deixar apenas a fonte de tensão alternada, exluindo a fonte de tensão contínua e abrindo o circuito no ramo onde está a fonte de corrente.
Desse modo, passando os elementos pro domínio da frequência:
Chegamos ao seguinte circuito modificado:
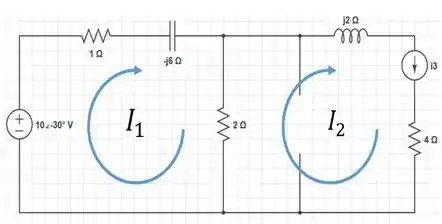
Vamos usar a lei das malhas para descobri o valor de .... Como podemos ver na figura acima, é a corrente de malha .
Aplicando a para a malha :
E aplicando a para a malha :
Subtituindo essa relação em , obtemos que:
Desse modo, a corrente é dada por:
Passo 5
Por fim, temos apenas que somar as correntes , e para obter a corrente :