Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 10.Problemas - Ex. 40

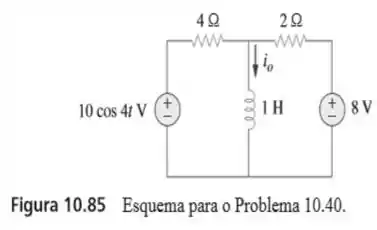
40. Determine i 0 no circuito apresentado na figura 10.85 usando superposição.

Passo 1

Fala galerinha! Bora pro nosso primeiro probleminha sobre superposição em circuitos C A .

Olha só! Nesse tipo de problema, há a presença de uma fonte de corrente de fonte contínua e outra de corrente alternada.

O que precisamos fazer pra esse caso, é calcular separadamente as contribuições de cada fonte e depois somar.

Quando digo contribuições, é somar a corrente naquele ramo do circuito gerada apenas pela fonte de tensão C C   com a corrente originada apenas pela fonte C A .

Vamos lá!

Passo 2

Primeiramente, vamos excluir a fonte de tensão C A e deixar apenas a fonte de tensão em corrente contínua C C .

Desse modo, o indutor vai se comportar como um curto circuito e o nosso circuito vai ficar com a seguinte cara:

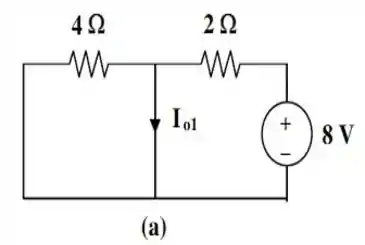
A corrente circulante, nesse caso, iremos chamar de I o 1 ...

Só que esse circuito tem algo bastante peculiar. O resistor de 4   Ω entá entre dois nós submetidos à mesma diferença de potencial. Logo, está situado num curto circuito e nenhua corrente vai passar por esse resistor.

I o 1 , então, vai ser igual à:

I o 1 = 8   V 2   Ω

I o 1 = 4   A

Passo 3

Agora, vamos tomar o caminho inverso. Excluimos a fonte de tensão C C e deixar apenas a fonte de tensão alternada ( C A ) .

Antes, vamos passar os elementos pro domínio da frequência:

10 cos ⁡ 4 t → 10 ∠ 0 °     ,   ω = 4   r a d / s

Desse modo, o nosso circuito vai ficar com a seguinte cara:

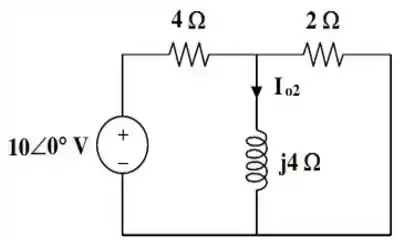
Em seguida, bora aplicar uma transformação de fontes nessa parte que inclui o resistor de 4   Ω e a fonte de tensão de 10 ∠ 0 °   V . Ficaremos com uma fonte de corrente e o mesmo resistor:

I = 10 ∠ 0 °   V 4   Ω

I = 2,5 ∠ 0 °   A

Aqui está o circuito modificado:

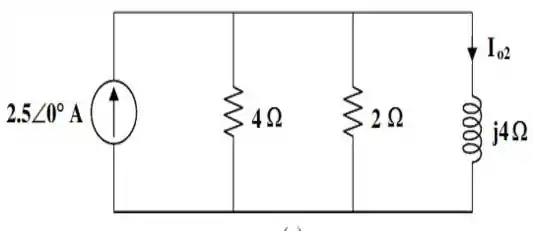
I o 2 pode então, ser facilmente obtida por divisão de corrente. Desse jeitinho aqui:

I o 2 = 4 | | 2   Ω [ 4 | | 2 + j 4 ]   Ω ⋅ 2,5 ∠ 0 °

I o 2 = 4 ⋅ 2 4 + 2 ⋅ 1 4 ⋅ 2 4 + 2 + j 4 ⋅ 2,5 ∠ 0 °

I o 2 = 4 3 4 3 + j 4 ⋅ 2,5 ∠ 0 °

I o 2 = 4 3 4,2164 ∠ 71,565 ° ⋅ 2,5 ∠ 0 °

I o 2 = 3,3333 ∠ 0 ° 4,2164 ∠ 71,565 °

I o 2 = 0,791 ∠ - 71,565 °

Passando pro domínio do tempo...

I o 2 = 0,791 cos ⁡ ( 4 t - 71,565 ° )

Passo 4

Pra finalizar, basta somar as correntes I o 2 e I o 1 e iremos obter i o :

i o = I o 1 + I o 2

i o = [ 4 + 0,791 cos ⁡ ( 4 t - 71,565 ° ) ]   A

Successfully Completed!

Resposta

i o = [ 4 + 0,791 cos ⁡ ( 4 t - 71,565 ° ) ]   A

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a tensão v em regime permanente, se v g = 2 cos ⁡ 2 tV .
Para o circuito fasorial correspondente, substitua tudo à esquerda dos terminais a - b por seu equivalente Thévenin e use o resultado para calcular a resposta forçada i .
No circuito fasorial do Ex. 14.3.2, com i g 2 = 0 , e v g 1 permanecendo inalterado, substitua tudo, exceto o capacitor, por seu equivalente de Thévenin e use o resultado para calcular V ( s ) , o fas
Resolva o Prob. 16.6 usando análise nodal, como descrito no Prob. 16.18.
10.30) Para o circuito fasorial correspondente ao Ex. 11.2.3, substitua tudo, exceto o resistor de 2-Ω entre os terminais c-d pelo seu equivalente de Thévenin e calcule a corrente i em regime permanen